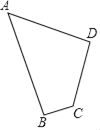
【题目】如图,四边形草坪ABCD中,∠B=90°,AB=24m,BC=7m,CD=15m,AD=20m.
(1)判断∠ADC是否是直角,并说明理由;
(2)试求四边形草坪ABCD的面积.
参考答案:
【答案】(1)∠D是直角,理由见解析;(2)234m2.
【解析】
(1)连接AC,先根据勾股定理求出AC的长,再求出AD的长,结合勾股定理的逆定理得到∠D是直角;
(2)由S四边形ABCD=S△ABC+S△ADC即可得出结论.
(1)∠D是直角,理由如下:
连接AC,
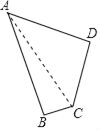
∵∠B=90°,AB=24m,BC=7m,
∴AC2=AB2+BC2=242+72=625,
∴AC=25(m).
又∵CD=15m,AD=20m,152+202=252,即AD2+DC2=AC2,
∴△ACD是直角三角形,或∠D是直角;
(2)S四边形ABCD=S△ABC+S△ADC
![]()
=234(m2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2;
(3)如果AC上有一点M(a,b)经过上述两次变换,那么对应A2C2上的点M2的坐标是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】一条排水管的截面如图所示.已知排水管的截面圆半径OB=10,截面圆圆心O到水面的距离OC是6,则水面宽AB是( )

A.16
B.10
C.8
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,分别以点A和点B为圆心,大于
 AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( )
AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( ) 
A.7
B.14
C.17
D.20 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).

(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值.
-
科目: 来源: 题型:
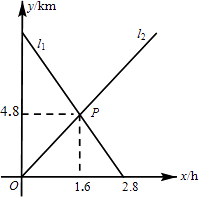
查看答案和解析>>【题目】小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离y(km)与已用时间x(h)之间的关系,则小敏、小聪行走的速度分别是( )
A.3km/h和4km/h
B.3km/h和3km/h
C.4km/h和4km/h
D.4km/h和3km/h -
科目: 来源: 题型:
查看答案和解析>>【题目】小聪和小明沿同一条笔直的马路同时从学校出发到某图书馆查阅资料,学校与 图书馆的路程是
 千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到 达图书馆,图中折线
千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到 达图书馆,图中折线  和线段
和线段  分别表示两人离学校的路程
分别表示两人离学校的路程  (千米)与所经过的 时间
(千米)与所经过的 时间  (分钟)之间的函数关系,请根据图像回答下列问题:
(分钟)之间的函数关系,请根据图像回答下列问题:(1)小聪在图书馆查阅资料的时间为 分钟;小聪返回学校的速度为 千米/分钟.
(2)请你求出小明离开学校的路程
 (千米)与所经过的时间
(千米)与所经过的时间  (分钟)之间的函数表达式;
(分钟)之间的函数表达式;(3)若设两人在路上相距不超过
 千米时称为可以“互相望见”,则小聪和小明可以“互相 望见”的时间共有多少分钟?
千米时称为可以“互相望见”,则小聪和小明可以“互相 望见”的时间共有多少分钟?
相关试题

