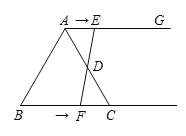
【题目】如图,在等边三角形ABC中,BC=6 cm,射线AG∥BC,点E从点A出发沿射线AG以1 cm/s的速度运动;同时点F从点B出发沿射线BC以2 cm/s的速度运动.设运动时间为t(s).
(1)△ABC的BC边上的高为_________cm;
(2)连接EF,当EF经过AC的中点D时,求证:△ADE≌△CDF;
(3)求当t为何值时,AC与EF互相平分;
(4)当t=________s时,四边形ACFE是菱形.
参考答案:
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() ;(4)6
;(4)6
【解析】
(1)根据等边三角形三线合一即可求解;
(2)由题意得到AD=CD,再由AG与BC平行,利用两直线平行内错角相等得到两对角相等,利用AAS即可得证;
(3)根据AC与EF互相平分,可得△ADE≌△CDF,可得AE=CF即![]() ,故可求解;
,故可求解;
(4)若四边形ACFE是菱形,则有CF=AC=AE=6,由E的速度求出E运动的时间即可.
解:(1)如图,过A点作AH⊥BC于H点
∵△ABC是等边三角形,BC=6 cm
∴BH=![]() BC=3cm
BC=3cm
∴AH=![]() =
=![]() cm
cm
故答案为:![]() .
.

(2)证明:∵AG∥BC,
∴∠EAD=∠DCF,∠AED=∠DFC,
∵D为AC的中点,
∴AD=CD,
在△ADE和△CDF中,
 ,
,
∴△ADE≌△CDF(AAS);
(3)若AC与EF互相平分,
则AD=CD,ED=FD,又∠ADE=∠CDF
∴△ADE≌△CDF.
∴AE=CF.
∴![]() .
.
解得![]() .
.
(4)若四边形ACFE是菱形,则有CF=AC=AE=6,
则此时的时间t=6÷1=6(s).
故答案为:6.
-
科目: 来源: 题型:
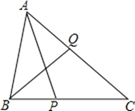
查看答案和解析>>【题目】如图,在△ABC中,
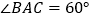 ,
,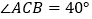 ,P、Q分别在BC、CA上,并且AP、BQ分别是∠BAC、∠ABC的角平分线.求证:
,P、Q分别在BC、CA上,并且AP、BQ分别是∠BAC、∠ABC的角平分线.求证:(1)
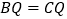 ;
;(2)
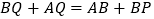 .
.
-
科目: 来源: 题型:
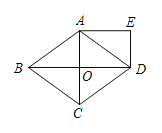
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形.
(2)若AB=5,BD=8,求矩形AODE的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
学习了无理数、二次根式及完全平方公式后,某数学兴趣小组开展了一次探究活动:
估算
 的近似值.
的近似值.小明的方法:
∵
 ,
,设
 (0<k<1),
(0<k<1),∴
 .
.∴
 ,
,∴
 ,
,解得
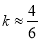 ,
,∴
 .
.(1)请你用小明的方法估算
 的近似值(结果保留两位小数);
的近似值(结果保留两位小数);(2)请你结合上述实例,概括出估算
 的公式:已知非负整数a,b,m,若
的公式:已知非负整数a,b,m,若 ,且
,且 ,则
,则 =_____________(用含a,b的代数式表示)
=_____________(用含a,b的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,
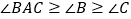 ,AD是BC边上的高,如果
,AD是BC边上的高,如果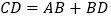 ,我们就称△ABC为“高和三角形”.请你依据这一定义回答问题:
,我们就称△ABC为“高和三角形”.请你依据这一定义回答问题:(1)若
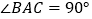 ,
,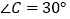 ,则△ABC____ “高和三角形”(填“是”或“不是”);
,则△ABC____ “高和三角形”(填“是”或“不是”);(2)一般地,如果△ABC是“高和三角形”,则
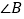 与
与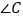 之间的关系是____,并证明你的结论
之间的关系是____,并证明你的结论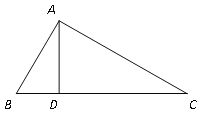
-
科目: 来源: 题型:
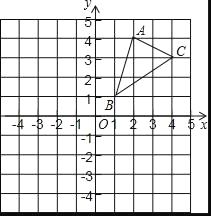
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2,并写出点A2、C2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知AB是圆O的直径,圆O过BC的中点D,且DE⊥AC.
(1)求证:DE是圆O的切线;
(2)若∠C=30°,CD=10cm,求圆O的半径.

相关试题

