【题目】如图,已知抛物线y=﹣ ![]() x2﹣
x2﹣ ![]() x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:令y=0得﹣ ![]() x2﹣
x2﹣ ![]() x+2=0,
x+2=0,
∴x2+2x﹣8=0,
x=﹣4或2,
∴点A坐标(2,0),点B坐标(﹣4,0),
令x=0,得y=2,∴点C坐标(0,2).
(2)
解:由图像①AB为平行四边形的边时,
∵AB=EF=6,对称轴x=﹣1,
∴点E的横坐标为﹣7或5,
∴点E坐标(﹣7,﹣ ![]() )或(5,﹣
)或(5,﹣ ![]() ),此时点F(﹣1,﹣
),此时点F(﹣1,﹣ ![]() ),
),
∴以A,B,E,F为顶点的平行四边形的面积=6× ![]() =
= ![]() .
.
②当点E在抛物线顶点时,点E(﹣1, ![]() ),设对称轴与x轴交点为M,令EM与FM相等,则四边形AEBF是菱形,此时以A,B,E,F为顶点的平行四边形的面积=
),设对称轴与x轴交点为M,令EM与FM相等,则四边形AEBF是菱形,此时以A,B,E,F为顶点的平行四边形的面积= ![]() ×6×
×6× ![]() =
= ![]() .
.
(3)
解:如图所示
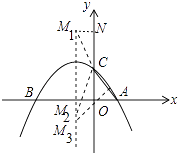
①当C为等腰三角形的顶角的顶点时,CM1=CA,CM2=CA,作M1N⊥OC于N,
在RT△CM1N中,CN= ![]() =
= ![]() ,
,
∴点M1坐标(﹣1,2+ ![]() ),点M2坐标(﹣1,2﹣
),点M2坐标(﹣1,2﹣ ![]() ).
).
②当M3为等腰三角形的顶角的顶点时,∵直线AC解析式为y=﹣x+2,
∴线段AC的垂直平分线为y=x与对称轴的交点为M3(﹣1.﹣1),
∴点M3坐标为(﹣1,﹣1).
③当点A为等腰三角形的顶角的顶点的三角形不存在.
综上所述点M坐标为(﹣1,﹣1)或(﹣1,2+ ![]() )或(﹣1,2﹣
)或(﹣1,2﹣ ![]() ).
).
【解析】(1)分别令y=0,x=0,即可解决问题.(2)由图像可知AB只能为平行四边形的边,分E点为抛物线上的普通点和顶点2种情况讨论,即可求出平行四边形的面积.(3)分A、C、M为顶点三种情形讨论,分别求解即可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上.
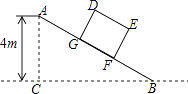
(1)求斜坡AB的水平宽度BC;
(2)矩形DEFG为长方体货柜的侧面图,其中DE=2.5m,EF=2m,将该货柜沿斜坡向上运送,当BF=3.5m时,求点D离地面的高.(结果保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.

(1)证明:∠E=∠C;
(2)若∠E=55°,求∠BDF的度数;
(3)设DE交AB于点G,若DF=4,cosB= ,E是
,E是  的中点,求EGED的值.
的中点,求EGED的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
(1)【特例探究】
如图1,当tan∠PAB=1,c=4 时,a= , b=;
时,a= , b=;
如图2,当∠PAB=30°,c=2时,a= , b=;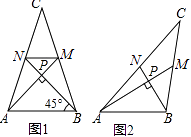
(2)【归纳证明】
请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.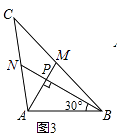
(3)【拓展证明】
如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3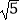 ,AB=3,求AF的长.
,AB=3,求AF的长.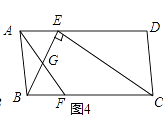
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂分发年终奖金,具体金额和人数如下表所示,则下列对这组数据的说法中不正确的是( )
人 数
1
3
5
70
10
8
3
金额(元)
200000
150000
80000
15000
10000
8000
5000
A.极差是195000
B.中位数是15000
C.众数是15000
D.平均数是15000 -
科目: 来源: 题型:
查看答案和解析>>【题目】矩形OABC有两边在坐标轴的正半轴上,如图所示,双曲线y=
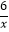 与边AB、BC分别交于D、E两点,OE交双曲线y=
与边AB、BC分别交于D、E两点,OE交双曲线y= 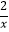 于点G,若DG∥OA,OA=3,则CE的长为( )
于点G,若DG∥OA,OA=3,则CE的长为( ) 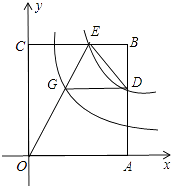
A.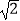
B.1.5
C.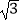
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=63°,那么∠B= .

相关试题

