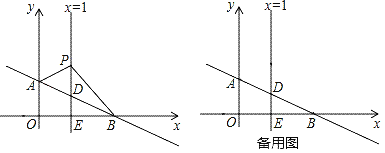
【题目】如图,平面直角坐标系中,直线AB交y轴于点A(0,1),交x轴于点B(3,0).直线x=1交AB于点D,交x轴于点E,P是直线x=1上一动点,在点D的上方,设P(1,n).
(1)求直线AB的解析式;
(2)求△ABP的面积(用含n的代数式表示);
(3)当S△ABP=2时,以PB为边在第一象限作等腰直角三角形BPC,求出点C的坐标.
参考答案:
【答案】(1)y=![]() x+1;(2)
x+1;(2)![]() ;(3)点C的坐标是(3,4)或(5,2)或(3,2).
;(3)点C的坐标是(3,4)或(5,2)或(3,2).
【解析】
(1)把![]() 的坐标代入直线
的坐标代入直线![]() 的解析式,即可求得
的解析式,即可求得![]() 的值,然后在解析式中,令
的值,然后在解析式中,令![]() ,求得
,求得![]() 的值,即可求得
的值,即可求得![]() 的坐标;
的坐标;
(2)利用![]() 即可求出结果;
即可求出结果;
(3)分三种情况讨论,当![]() 、
、![]() 、
、![]() 分别为等腰直角三角形
分别为等腰直角三角形![]() 的直角顶点时,求出
的直角顶点时,求出![]() 点的坐标分别为
点的坐标分别为![]() 、
、![]() 、
、![]() 。
。
(1)设直线AB的解析式是y=kx+b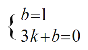
把A(0,1),B(3,0)代入得:
解得: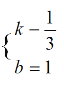
∴直线AB的解析式是:![]()
(2)过点A作AM⊥PD,垂足为M,则有AM=1,
∵x=1时,![]() =
=![]() ,P在点D的上方,
,P在点D的上方,
∴PD=n﹣![]() ,
,![]()
由点B(3,0),可知点B到直线x=1的距离为2,即△BDP的边PD上的高长为2,
∴![]() ,
,
∴![]() ;
;
(3)当S△ABP=2时,![]() ,解得n=2,∴点P(1,2).
,解得n=2,∴点P(1,2).
∵E(1,0), ∴PE=BE=2,
∴∠EPB=∠EBP=45°.
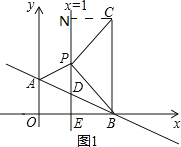
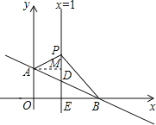
第1种情况,如图1,∠CPB=90°,BP=PC,
过点C作CN⊥直线x=1于点N.
∵∠CPB=90°,∠EPB=45°,
∴∠NPC=∠EPB=45°.
又∵∠CNP=∠PEB=90°,BP=PC,
∴△CNP≌△BEP,∴PN=NC=EB=PE=2,
∴NE=NP+PE=2+2=4, ∴C(3,4).
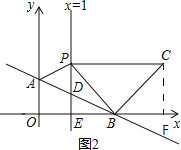
第2种情况,如图2, ∠PBC=90°,BP=BC,
过点C作CF⊥x轴于点F.
∵∠PBC=90°,∠EBP=45°,
∴∠CBF=∠PBE=45°.
又∵∠CFB=∠PEB=90°,BC=BP,
∴△CBF≌△PBE.
∴BF=CF=PE=EB=2,
∴OF=OB+BF=3+2=5, ∴C(5,2).
3种情况,如图3,∠PCB=90°,
∴∠CPB=∠EBP=45°,
![]()
∴△PCB≌△ BEP,
∴PC=CB=PE=EB=2,∴C(3,2).
∴以PB为边在第一象限作等腰直角三角形BPC,
综上所述点C的坐标是(3,4)或(5,2)或(3,2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知∠DAB=∠DCB,AF平分∠DAB,CE平分∠DCB,∠FCE=∠CEB,试说明:AF∥CE。

解:(1)因为∠DAB=∠DCB( ),
又AF平分∠DAB,
所以_____=
 ∠DAB( ),
∠DAB( ),又因为CE平分∠DCB,
所以∠FCE=_____( ),
所以∠FAE=∠FCE。
因为∠FCE=∠CEB,
所以______=________
所以AF∥CE( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两种客车共7辆,已知甲种客车载客量是30人,乙种客车载客量是45人.其中,每辆乙种客车租金比甲种客车多100元,5辆甲种客车和2辆乙种客车租金共需2300元.
(1)租用一辆甲种客车、一辆乙种客车各多少元?
(2)设租用甲种客车x辆,总租车费为y元,求y与x的函数关系;在保证275名师生都有座位的前提下,求当租用甲种客车多少辆时,总租车费最少,并求出这个最少费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
(1)求证:△DEC≌△EDA;
(2)求DF的值;
(3)在线段AB上找一点P,连结FP使FP⊥AC,连结PC,试判定四边形APCF的形状,并说明理由,直接写出此时线段PF的大小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,
 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )

A. AB//DC,AD//BC B. AB//DC,AD=BC
C. AO=CO,BO=DO D. AB=DC,AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市团委举行以“我的中国梦”为主题的知识竞赛,甲、乙两所学校的参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如图不完整的统计图表:
乙校成绩统计表
分数
 分
分
人数
 人
人
70
7
80
______
90
1
100
8
 乙学校的参赛人数是______人
乙学校的参赛人数是______人
 在图
在图 中,“80分”所在扇形的圆心角度数为______;
中,“80分”所在扇形的圆心角度数为______;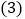 请你将图
请你将图 补充完整;
补充完整;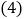 求乙校成绩的平均分.
求乙校成绩的平均分.
相关试题

