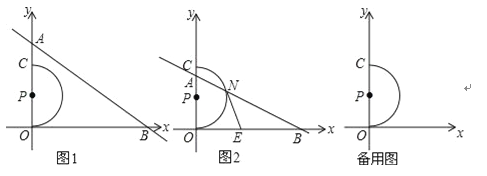
【题目】已知,在平面直角坐标系中,点P(0,2),以P为圆心,OP为半径的半圆与y轴的另一个交点是C,一次函数y=﹣![]() x+m(m为实数)的图象为直线l,l分别交x轴,y轴于A,B两点,如图1.
x+m(m为实数)的图象为直线l,l分别交x轴,y轴于A,B两点,如图1.
(1)B点坐标是 (用含m的代数式表示),∠ABO= °;
(2)若点N是直线AB与半圆CO的一个公共点(两个公共点时,N为右侧一点),过点N作⊙P的切线交x轴于点E,如图2.
①是否存在这样的m的值,使得△EBN是直角三角形?若存在,求出m的值;若不存在,请说明理由.
②当![]() 时,求m的值.
时,求m的值.
参考答案:
【答案】(1)![]() ,30;(2)m=2或3;(3)m=
,30;(2)m=2或3;(3)m=![]() .
.
【解析】
试题分析:(1)首先求出直线与x轴交点坐标,进而得出答案,再利用锐角三角函数关系得出∠ABO的度数;
(2)①分别利用∠NEB=90°和∠ENB=90°,结合切线的性质得出m的值;
②首先求出NG:EN=![]() ,再得出△PHN∽△NGE,再利用相似三角形的性质,进而得出m的值.
,再得出△PHN∽△NGE,再利用相似三角形的性质,进而得出m的值.
试题解析:(1)当y=0,则0=﹣![]() x+m,
x+m,
解得:x=![]() m,
m,
故B点坐标是![]() (用含m的代数式表示),
(用含m的代数式表示),
∵一次函数y=﹣![]() x+m与y轴交于点(0,m),
x+m与y轴交于点(0,m),
∴tan∠ABO=![]() =
=![]() ,
,
∴∠ABO=30°;
故答案为:![]() ,30;
,30;
(2)①如图①,假设存在这样的m的值,使得△EBN是直角三角形.连接NP
若∠NEB=90°,∵NE是⊙P的切线,
∴∠PNE=90°,
∵∠POE=90°,
∴四边形OPNE是矩形,
∴PN=2,∠APN=90°,
在Rt△APN中,PN=2,∠BAO=60°,
∴PA=1,
∴m=3,
若∠ENB=90°,∵NE是⊙P的切线,
∴∠PNE=90°,
∴点P、N、B三点共线,即点P与点A重合,
∴m=2,
综上可知,m=2或3;
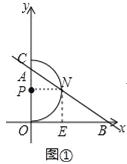
②如图②,连接PN,过点E作,EG⊥AB于G,过点P作,PH⊥AB于H,
则PA=m﹣2,PH=![]() ,
,
∵![]() ,∴EB=
,∴EB=![]() ,EN=EO=
,EN=EO=![]() ,EG=
,EG=![]() ,
,
∴EG:EN=1:4,∴NG:EN=![]() ,
,
∵∠PNE=90°,∴∠PNH+∠ENG=90°,
∵∠GNE+∠NEG=90°,
∴∠NEG=∠PNH,
∵∠PHN=∠EGN=90°,
∴△PHN∽△NGE,
∴![]() ,
,
∴ ,
,
解得:m=![]() .
.
-
科目: 来源: 题型:
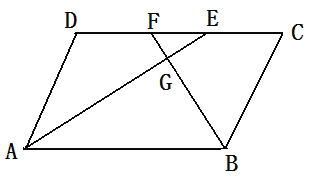
查看答案和解析>>【题目】平行四边形ABCD中, AE、BF分别平分∠DAB和∠ABC交CD于点E、F.AE、BF交于点G.
(1)求证AE⊥BF
(2)判断DE和CF的大小关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校组织340名师生进行长途考察活动,带有行李170件,计划租用甲、乙两种型号的汽车共10辆.经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.
(1)请你帮助学校设计所有可行的租车方案.
(2)如果甲车的租金为每辆2 000元,乙车的租金为每辆1 800元,问哪种可行方案使租车费用最省?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=BD;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为4cm,E为CD边的中点,,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于__________cm.
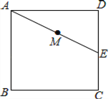
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图下图所示,已知AB//CD, ∠B=30°,∠D=120°;

(1)若∠E=60°,则∠E=______;
(2)请探索∠E与∠F之间满足的数量关系?说明理由.
(3)如下图所示,已知EP平分∠BEF,FG平分∠EFD,反向延长FG交EP于点P,求∠P的度数;
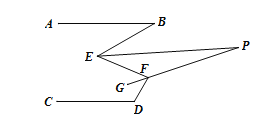
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,己知△ABC中,∠C=90°,∠A=30°,AC=
 .动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为 .
.动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为 .
相关试题

