【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,有下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴是x=1;
③抛物线与x轴有两个交点,它们之间的距离是 ![]() ;
;
④在对称轴左侧y随x增大而增大.
其中正确的说法是( )
A.①②③
B.②③④
C.②③
D.①④
参考答案:
【答案】D
【解析】解:∵抛物线过点(﹣2,0)和(0,6),则 ![]() ,解得
,解得 ![]() ,
,
∴抛物线的解析式为y=﹣x2+x+6,
∴抛物线与y轴的交点为(0,6),故①正确;
抛物线的对称是:直线x=﹣ ![]() =
= ![]() ,故②错误;
,故②错误;
抛物线与x轴的两个交点为(﹣2,0),(3,0),它们之间的距离是5,故③错误;
抛物线开口向下,则在对称轴左侧,y随x的增大而增大,故④正确.
正确答案为①④.
故选:D.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD平分∠BAC,EG⊥AD于H,则下列等式中成立的是 ( )
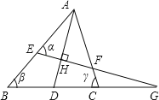
A. ∠α=
 (∠β﹣∠γ) B. ∠α=
(∠β﹣∠γ) B. ∠α= (∠β+∠γ) C. ∠G=
(∠β+∠γ) C. ∠G= (∠β+∠γ) D. ∠G=
(∠β+∠γ) D. ∠G= ∠α
∠α -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
x
…
﹣2
﹣1
0
1
2
…
y
…
0
4
6
6
4
…
从上表可知,有下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴是x=1;
③抛物线与x轴有两个交点,它们之间的距离是 ;
;
④在对称轴左侧y随x增大而增大.
其中正确的说法是( )
A.①②③
B.②③④
C.②③
D.①④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是半圆,连接AB,点O为AB的中点,点C,D在
是半圆,连接AB,点O为AB的中点,点C,D在  上,连接AD,CO,BC,BD,OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )
上,连接AD,CO,BC,BD,OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( ) 
A.26°
B.28°
C.30°
D.32° -
科目: 来源: 题型:
查看答案和解析>>【题目】小强掷两枚质地均匀的骰子,每个骰子的六个面上分别刻有1到6的点数,则两枚骰子点数相同的概率为
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰Rt△ABC中,∠C=90°,D为AC上一点,连接BD,将线段BD绕点D顺时针旋转90°得到线段DE,DE与AB相交于点F,过点D作DG⊥AB,垂足为点G.若EF=5,CD=2
 ,则△BDG的面积为 .
,则△BDG的面积为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知C是∠AOB的平分线上一点,点P,P′分别在边OA,OB上,如果要得到OP=OP′,需要添加以下条件中的某一个,那么所有可能结果的序号为________.
①∠OCP=∠OCP′;②∠OPC=∠OP′C;③PC=P′C;④PP′⊥OC.
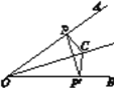
相关试题

