【题目】如图,直线l1、l2、l3分别过正方形ABCD的三个顶点A,B,D,且相互平行,若l1与l2的距离为1,l2与l3的距离为1,则该正方形的面积是 . 
参考答案:
【答案】5
【解析】解:过点B作BE⊥l1于E,过点D作DF⊥l1于F, 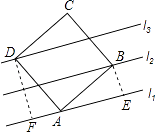
∵l1与l2的距离为1,l2与l3的距离为1,l1∥l2∥l3 ,
∴DF=2,BE=1,∠DFA=∠AEB=90°,
∴∠ADF+∠DAF=90°,
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∴∠DAF+∠BAE=90°,
∴∠ADF=∠BAE,
在△ADF和△BAE中,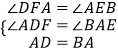 ,
,
∴△ADF≌△BAE(AAS)
∴AE=DF=2,
在Rt△ABE中,AB2=AE2+BE2=12+22=5,
∴S正方形ABCD=5.
所以答案是:5.
【考点精析】掌握平行线之间的距离和勾股定理的概念是解答本题的根本,需要知道两条平行线的距离:两条直线平行,从一条直线上的任意一点向另一条直线引垂线,垂线段的长度,叫做两条平行线的距离;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(a,1)、B(﹣1,b)都在双曲线y=﹣
 上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是( )
上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是( )
A.y=x
B.y=x+1
C.y=x+2
D.y=x+3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知,在△ABC中,∠ACB=90°,AC=BC,点D是AB边上的中点,点M和点N是动点,分别从A,C出发,以相同的速度沿AC,CB边上运动.
(1)判断DM与DN的关系,并说明理由;
(2)若AC=BC=2,请直接写出四边形MCND的面积;
(3)如图②,当点M运动到C点后,将改变方向沿着CB运动,此时,点N在CB延长线上,过M作ME⊥CD于点E,过点N作NF⊥DB交DB延长线于F,求证:ME=NF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是AB中点,联结CD.

(1)若AB=10且∠ACD=∠B,求AC的长.
(2)过D点作BC的平行线交AC于点E,设 =
=  ,
,  =
=  ,请用向量
,请用向量  、
、  表示
表示  和
和  (直接写出结果)
(直接写出结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数y=
 (a>0,a为常数)和y=
(a>0,a为常数)和y=  在第一象限内的图象如图所示,点M在y=
在第一象限内的图象如图所示,点M在y=  的图象上,MC⊥x轴于点C,交y=
的图象上,MC⊥x轴于点C,交y=  的图象于点A;MD⊥y轴于点D,交y=
的图象于点A;MD⊥y轴于点D,交y=  的图象于点B,当点M在y=
的图象于点B,当点M在y=  的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是 .
的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是 . 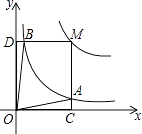
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图中所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D的边长分别是12,16,9,12,则最大正方形E的面积是_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,CD⊥AB于点D,⊙D经过点B,与BC交于点E,与AB交与点F.已知tanA=
 ,cot∠ABC=
,cot∠ABC=  ,AD=8.
,AD=8.
(1)求⊙D的半径;
(2)求CE的长.
相关试题

