【题目】如图,在△ABC中,AB=AC=10,sinB=![]() ,
,
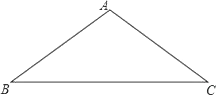
(1)求边BC的长;
(2)将△ABC绕着点C旋转得△A′B′C,点A的对应点A′,点B的对应点B′.如果点A′在BC边上,那么点B和点B′之间的距离等于多少?
参考答案:
【答案】(1)16(2)![]()
【解析】(1)AD⊥BC于点D,由等腰三角形的性质可得BC=2BD,在Rt△ABD中根据AD=ABsinB得出AD,再根据勾股定理即可得BD,从而得出答案;
(2)B′E⊥BC于点E,由旋转的性质得B′C=BC=16,∠ABC=∠ACB=∠A′CB′,在Rt△B′CE中求出B′E、CE的长,由BC=16可得BE的长,继而根据勾股定理可得答案.
(1)解:如图,过点A作AD⊥BC于点D,
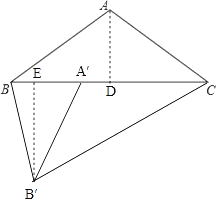
∵AB=AC=10,
∴BC=2BD,
在Rt△ABD中,∵sinB= ![]() ,
,
∴AD=ABsinB=10× ![]() =6,
=6,
∴BD= ![]() =8,
=8,
则BC=2BD=16;
(2)解:过点B′作B′E⊥BC于点E, 根据题意知B′C=BC=16,∠ABC=∠ACB=∠A′CB′,
∴sin∠BCB′=sinB= ![]() ,
,
∴B′E=B′Csin∠BCB′=16× ![]() =
= ![]() ,
,
∴CE= ![]() =
= ![]() ,
,
又∵BC=16,
∴BE=BC﹣CE=16﹣ ![]() =
= ![]() ,
,
∴BB′= ![]() =
= ![]() =
= ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点P、Q分别是BC、AC边上的点,PS
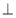 AC,PR
AC,PR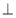 AB,若
AB,若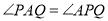 ,PR
,PR PS,则下列结论:①PA平分
PS,则下列结论:①PA平分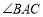 ,②AS
,②AS AR;③QP∥AR;④△BRP≌△CPS;其中正确的结论有( )
AR;③QP∥AR;④△BRP≌△CPS;其中正确的结论有( )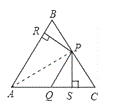
A. 4个B. 3个C. 2个D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中AD是∠A的外角平分线,P是AD上一动点且不与点A、D重合,记PB+PC=a,AB+AC=b,则a、b的大小关系是( )
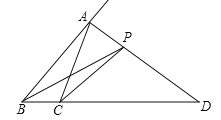
A.a>b B.a=b C.a<b D.不能确定
-
科目: 来源: 题型:
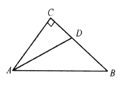
查看答案和解析>>【题目】如图,在
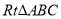 中,
中,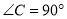 ,
,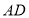 平分
平分 交
交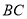 于点
于点 .
.
(1)若BC=7,BD=4,则点
 到
到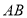 的距离是________;
的距离是________;(2)若
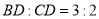 ,点
,点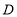 到
到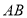 的距离是8,则
的距离是8,则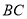 的长是________.
的长是________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,当一个点到达终点时另一个点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒,则当t=______秒时,△PEC与△QFC全等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学的高中部在A校区,初中部在B校区,学校学生会计划在3月12日植树节当天安排部分学生到郊区公园参加植树活动.已知A校区的每位高中学生往返车费是6元,B校区的每位初中学生往返的车费是10元,要求初、高中均有学生参加,且参加活动的初中学生比参加活动的高中学生多4人,本次活动的往返车费总和不超过210元,求初、高中最多各有多少学生参加.
-
科目: 来源: 题型:
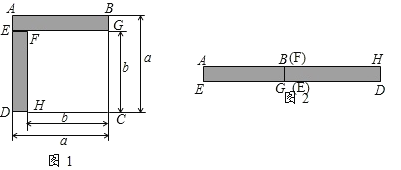
查看答案和解析>>【题目】解决问题:
(1)如图1,已知正方形
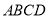 的边长为
的边长为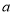 ,正方形
,正方形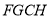 的边长为
的边长为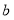 ,长方形
,长方形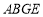 和
和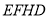 为阴影部分,则阴影部分的面积是____.(写成平方差的形式)
为阴影部分,则阴影部分的面积是____.(写成平方差的形式)(2)将图1中的长方形
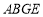 和
和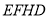 剪下来,拼成图2所示的长方形,则长方形
剪下来,拼成图2所示的长方形,则长方形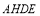 的面积是____.(写成多项式相乘的形式)
的面积是____.(写成多项式相乘的形式)(3)比较图1与图2的阴影部分的面积,可得乘法公式____.
(4)利用所得公式计算:
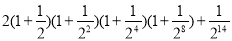
相关试题

