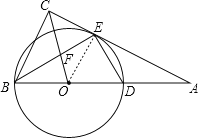
【题目】如图,在Rt△ABC中,∠ACB=90°,以斜边AB上一点O为圆心,OB为半径作⊙O,交AC于点E,交AB于点D,且∠BEC=∠BDE.

(1)求证:AC是⊙O的切线;
(2)连接OC交BE于点F,若![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OE,证得OE⊥AC即可确定AC是切线;
(2)根据OE∥BC,分别得到△AOE∽△ACB和△OEF∽△CBF,利用相似三角形对应边的比相等找到中间比即可求解.
解:(1)证明:连接OE,
∵OB=OE,
∴∠OBE=∠OEB,
∵∠ACB=90°,
∴∠CBE+∠BEC=90°,
∵BD为⊙O的直径,
∴∠BED=90°,
∴∠DBE+∠BDE=90°,
∴∠CBE=∠DBE,
∴∠CBE=∠OEB,
∴OE∥BC,
∴∠OEA=∠ACB=90°,
即OE⊥AC,
∴AC为⊙O的切线;
(2)∵OE∥BC,∴△AOE∽△ABC,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵OE∥BC,
∴△OEF∽△CBF,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠1和∠2是同旁内角,∠1=40°,∠2等于( )
A. 160° B. 140° C. 40° D. 无法确定
-
科目: 来源: 题型:
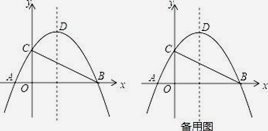
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2﹣3ax﹣4a的图象经过点C(0,2),交x轴于点A、B(A点在B点左侧),顶点为D.
(1)求抛物线的解析式及点A、B的坐标;
(2)将△ABC沿直线BC对折,点A的对称点为A′,试求A′的坐标;
(3)抛物线的对称轴上是否存在点P,使∠BPC=∠BAC?若存在,求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形纸片内有100个点,连同三角形的顶点共103个点,其中任意三点都不共线.现以这些点为顶点作三角形,并把纸片剪成小三角形,这样的小三角形的个数是( )
A. 299 B. 201 C. 205 D. 207
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.

(1)试判断△BDE的形状,并说明理由;
(2)若AB=4,AD=8,求△BDE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下列各组线段为边,能组成三角形的是( )
A. 2,2,4 B. 2,3,6 C. 1,2,3 D. 3,4,5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“喜爱哪种动物的同学最多”的调查活动中,调查了全班60名同学,其中喜欢大熊猫的同学占70%,则喜欢大熊猫的学生人数是( ).
A. 42 B. 45 C. 60 D. 75
相关试题

