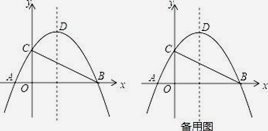
【题目】如图,在平面直角坐标系中,抛物线y=ax2﹣3ax﹣4a的图象经过点C(0,2),交x轴于点A、B(A点在B点左侧),顶点为D.
(1)求抛物线的解析式及点A、B的坐标;
(2)将△ABC沿直线BC对折,点A的对称点为A′,试求A′的坐标;
(3)抛物线的对称轴上是否存在点P,使∠BPC=∠BAC?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)A(﹣1,0),B(4,0).(2)A'(1,4);(3)P的坐标为(![]() ,-
,-![]() )或(
)或(![]() ,2+
,2+![]() ).
).
【解析】试题分析:(1)将(0,2)代入抛物线解析式求得a的值,从而得出抛物线的解析式,再令y=0,得出x的值,即可求得点A、B的坐标;
(2)如图2,作A'H⊥x轴于H,可证明△AOC∽△COB,得出∠ACO=∠CBO,由A'H∥OC,即可得出A′H的长,即可求得A′的坐标;
(3)分两种情况:①如图3,以AB为直径作⊙M,⊙M交抛物线的对称轴于P(BC的下方),由圆周角定理得出点P坐标;②如图4,类比第(2)小题的背景将△ABC沿直线BC对折,点A的对称点为A',以A'B为直径作⊙M',⊙M'交抛物线的对称轴于P'(BC的上方),作M'E⊥A'H于E,交对称轴于F,求得M'F,在Rt△M'P'F中,由勾股定理得出P'F得的长,从而得出点P的坐标即可.
解:(1)把C(0,2)代入y=ax2﹣3ax﹣4a得﹣4a=2,
解得![]() .
.
所以抛物线的解析式为![]() .
.
令![]() ,可得:x1=﹣1,x2=4.
,可得:x1=﹣1,x2=4.
所以A(﹣1,0),B(4,0).
(2)如图2,作A'H⊥x轴于H,
因为![]() ,且∠AOC=∠COB=90°,
,且∠AOC=∠COB=90°,
所以△AOC∽△COB,
所以∠ACO=∠CBO,可得∠ACB=∠OBC+∠BCO=90°,
由A'H∥OC,AC=A'C得OH=OA=1,A'H=2OC=4;
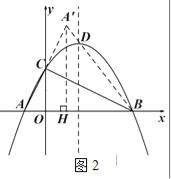
所以A'(1,4);
(3)分两种情况:
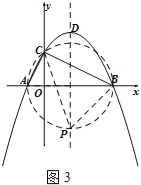
①如图3,以AB为直径作⊙M,⊙M交抛物线的对称轴于P(BC的下方),
由圆周角定理得∠CPB=∠CAB,
易得:MP=![]() AB.所以P(
AB.所以P(![]() ,
,![]() ).
).
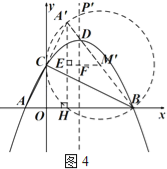
②如图4,类比第(2)小题的背景将△ABC沿直线BC对折,
点A的对称点为A',以A'B为直径作⊙M',⊙M'交抛物线的对称轴于P'(BC的上方),
则∠CP2B=∠CA'B=∠CAB.
作M'E⊥A'H于E,交对称轴于F.
则M'E=![]() BH=
BH=![]() ,EF=
,EF=![]() =
=![]() .
.
所以M'F=![]() =1.
=1.
在Rt△M'P'F中,P'F=![]() ,
,
所以P'M=2+![]() .
.
所以P'(![]() ,2+
,2+![]() ).
).
综上所述,P的坐标为(![]() ,
,![]() )或(
)或(![]() ,2+
,2+![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(-3,5)所在的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(3,﹣2)关于y轴的对称点是_________,关于原点的对称点是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠1和∠2是同旁内角,∠1=40°,∠2等于( )
A. 160° B. 140° C. 40° D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形纸片内有100个点,连同三角形的顶点共103个点,其中任意三点都不共线.现以这些点为顶点作三角形,并把纸片剪成小三角形,这样的小三角形的个数是( )
A. 299 B. 201 C. 205 D. 207
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,以斜边AB上一点O为圆心,OB为半径作⊙O,交AC于点E,交AB于点D,且∠BEC=∠BDE.

(1)求证:AC是⊙O的切线;
(2)连接OC交BE于点F,若
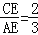 ,求
,求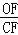 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.

(1)试判断△BDE的形状,并说明理由;
(2)若AB=4,AD=8,求△BDE的面积.
相关试题

