【题目】如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=5,DA=5 ![]() ,则BD的长为 .
,则BD的长为 . 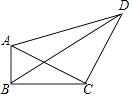
参考答案:
【答案】![]()
【解析】解:作DM⊥BC,交BC延长线于M,如图所示:
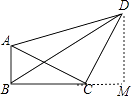
则∠M=90°,
∴∠DCM+∠CDM=90°,
∵∠ABC=90°,AB=3,BC=4,
∴AC2=AB2+BC2=25,
∴AC=5,
∵AD=5 ![]() ,CD=5,
,CD=5,
∴AC2+CD2=AD2,
∴△ACD是直角三角形,∠ACD=90°,
∴∠ACB+∠DCM=90°,
∴∠ACB=∠CDM,
∵∠ABC=∠M=90°,
∴△ABC∽△CMD,
∴ ![]() =
= ![]() =
= ![]() =1,
=1,
∴CM=AB=3,DM=BC=4,
∴BM=BC+CM=7,
∴BD= ![]() =
= ![]() =
= ![]() ,
,
故答案为: ![]() .
.
作DM⊥BC,交BC延长线于M,由勾股定理得出AC2=AB2+BC2=25,求出AC2+CD2=AD2,由勾股定理的逆定理得出△ACD是直角三角形,∠ACD=90°,证出∠ACB=∠CDM,得出△ABC∽△CMD,由相似三角形的对应边成比例求出CM=AB=3,DM=BC=4,得出BM=BC+CM=7,再由勾股定理求出BD即可
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各数中比1大的数是( )
A.2
B.0
C.﹣1
D.﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】某市一湖的湖心岛有一颗百年古树,当地人称它为“乡思柳”,不乘船不易到达,每年初春时节,人们喜欢在“聚贤亭”观湖赏柳.小红和小军很想知道“聚贤亭”与“乡思柳”之间的大致距离,于是,有一天,他们俩带着侧倾器和皮尺来测量这个距离.测量方法如下:如图,首先,小军站在“聚贤亭”的A处,用侧倾器测得“乡思柳”顶端M点的仰角为23°,此时测得小军的眼睛距地面的高度AB为1.7米,然后,小军在A处蹲下,用侧倾器测得“乡思柳”顶端M点的仰角为24°,这时测得小军的眼睛距地面的高度AC为1米.请你利用以上测得的数据,计算“聚贤亭”与“乡思柳”之间的距离AN的长(结果精确到1米).(参考数据:sin23°≈0.3907,cos23°≈0.9205,tan23°≈0.4245,sin24°≈0.4067,cos24°≈0.9135,tan24°≈0.4452.)
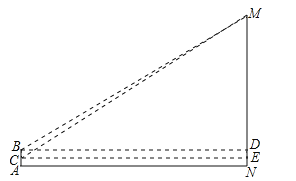
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形一边长是10cm,一边长是6cm,则它的第三边x的取值范围是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的半径长为1,AB、AC是⊙O的两条弦,且AB=AC,BO的延长线交AC于点D,联结OA、OC.
(1)求证:△OAD∽△ABD;
(2)当△OCD是直角三角形时,求B、C两点的距离;
(3)记△AOB、△AOD、△COD 的面积分别为S1、S2、S3,如果S2是S1和S3的比例中项,求OD的长.
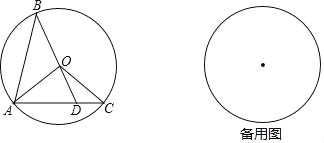
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=15cm,点E在AD上,且AE=9cm,连接EC,将矩形ABCD沿直线BE翻折,点A恰好落在EC上的点A′处,则A′C=cm.
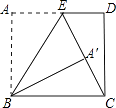
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( )
A. 等腰三角形是轴对称图形
B. 三角相等的三角形是等边三角形
C. 如果两个三角形成轴对称,那么这两个三角形一定全等
D. 若A,B两点关于直线MN对称,则AB垂直平分MN
相关试题

