【题目】如图,数轴上点A表示的数为﹣2,点B表示的数为8,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
(1)填空:
①A、B两点间的距离AB= ,线段AB的中点表示的数为 ;
②用含t的代数式表示:t秒后,点P表示的数为 ;点Q表示的数为 .
(2)求当t为何值时,PQ=![]() AB;
AB;
(3)当点P运动到点B的右侧时,PA的中点为M,N为PB的三等分点且靠近于P点,求PM﹣![]() BN的值.
BN的值.
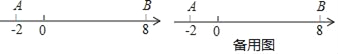
参考答案:
【答案】(1)①10,3;②﹣2+3t,8﹣2t;(2)t=1或3;(3)5
【解析】
(1)①根据点A表示的数为﹣2,点B表示的数为8,即可得到A、B两点间的距离以及线段AB的中点表示的数;②依据点P,Q的运动速度以及方向,即可得到结论;
(2)由t秒后,点P表示的数﹣2+3t,点Q表示的数为8﹣2t,于是得到PQ=|(﹣2+3t)﹣(8﹣2t)|=|5t﹣10|,列方程即可得到结论;
(3)依据PA的中点为M,N为PB的三等分点且靠近于P点,运用线段的和差关系进行计算,即可得到PM﹣![]() BN的值.
BN的值.
解:(1)①8﹣(﹣2)=10,﹣2+![]() ×10=3,
×10=3,
②由题可得,点P表示的数为﹣2+3t,点Q表示的数为8﹣2t;
(2)∵t秒后,点P表示的数﹣2+3t,点Q表示的数为8﹣2t,
∴PQ=|(﹣2+3t)﹣(8﹣2t)|=|5t﹣10|,
又PQ=![]() AB=
AB=![]() ×10=5,
×10=5,
∴|5t﹣10|=5,
解得:t=1或3,
∴当t=1或3时,PQ=![]() AB;
AB;
(3)∵PA的中点为M,N为PB的三等分点且靠近于P点,
∴MP=![]() AP=
AP=![]() ×3t=
×3t=![]() t,
t,
BN=![]() BP=
BP=![]() (AP﹣AB)=
(AP﹣AB)=![]() ×(3t﹣10)=2t﹣
×(3t﹣10)=2t﹣![]() ,
,
∴PM﹣![]() BN=
BN=![]() t﹣
t﹣![]() (2t﹣
(2t﹣![]() )=5.
)=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为____.

-
科目: 来源: 题型:
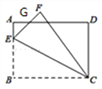
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,BC=8,E为AB上一点,将△BCE沿CE翻折至△FCE,EF与AD相交于点G,且AG=FG,则线段AE的长为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 ﹣(π﹣3)0﹣(﹣1)2017+(﹣
﹣(π﹣3)0﹣(﹣1)2017+(﹣  )﹣2+tan60°+|
)﹣2+tan60°+|  ﹣2|
﹣2| -
科目: 来源: 题型:
查看答案和解析>>【题目】已知y+3和2x-1成正比例,且x=2时,y=1。
(1)写出y与x的函数解析式。
(2)当0≤x≤3 时,y的最大值和最小值分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
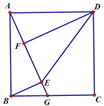
(1)求证:△ABE≌△DAF;
(2)若BE=8,EF=7,求CD的长.
-
科目: 来源: 题型:
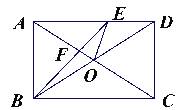
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线AC、BD交于点O,BE平分∠ABC交AC于点F,交AD于点E,且∠DBF=15°,求证:(1)AO=AE; (2)∠FEO的度数.
相关试题

