【题目】已知二次函数y=a(x+2)2+3(a<0)的图象如图所示,则以下结论:①当x>﹣2时,y随x的增大而增大;②不论a为任何负数,该二次函数的最大值总是3;③当a=﹣1时,抛物线必过原点;④该抛物线和x轴总有两个公共点.其中正确结论是( )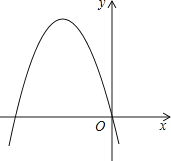
A.①②
B.②③
C.②④
D.①④
参考答案:
【答案】C
【解析】解:根据解析式可以得到函数的顶点坐标是(﹣2,3),对称轴是直线x=﹣2,
则当x>﹣2时,y随x的增大而减小,故①错误;
顶点坐标是(﹣2,3),开口向下,则函数的最大值是3,则②正确;
当a=﹣1时,函数的解析式是:y=﹣(x+2)2+3,(0,0)不满足函数的解析式,故函数不经过原点,故③错误;
顶点坐标是(﹣2,3),开口向下,则该抛物线和x轴总有两个公共点,故④正确.
故选C.
【考点精析】通过灵活运用二次函数的性质和二次函数图象以及系数a、b、c的关系,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,∠D=100°,AC平分∠BCD,且∠ACB=40°,∠BAC=70°.

(1)AD与BC平行吗?试写出推理过程;
(2)求∠DAC和∠EAD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AB=20,AC=15,BC边上的高为12,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸每个小方格是边长为1个单位长度的正方形,在平面直角坐标系中,点A(1,0),B(5,0),C(a,b)D(1,4).
(1)描出A、B、C、D四点的位置.如图,则a= ;b= ;
(2)四边形ABCD的面积是 ;(直接写出结果)
(3)把四边形ABCD向左平移6个单位,再向下平移1个单位得到四边形A'B'C'D',在图中画出四边形A'B'C'D',并写出A'B'C'D'的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016湖南省株洲市)某市对初二综合素质测评中的审美与艺术进行考核,规定如下:考核综合评价得分由测试成绩(满分100分)和平时成绩(满分100分)两部分组成,其中测试成绩占80%,平时成绩占20%,并且当综合评价得分大于或等于80分时,该生综合评价为A等.
(1)孔明同学的测试成绩和平时成绩两项得分之和为185分,而综合评价得分为91分,则孔明同学测试成绩和平时成绩各得多少分?
(2)某同学测试成绩为70分,他的综合评价得分有可能达到A等吗?为什么?
(3)如果一个同学综合评价要达到A等,他的测试成绩至少要多少分?
-
科目: 来源: 题型:
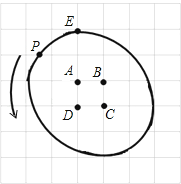
查看答案和解析>>【题目】在每个小正方形的边长均为1的7×7网格图中,格点上有A,B,C,D,E五个定点,如图所示,一个动点P从点E出发,绕点A逆时针旋转90°,之后该动点继续绕点B,C,D逆时针90°后回到初始位置,点P运转路线的总长是 . (结果保留π)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2016次运动后,动点P的坐标是( )
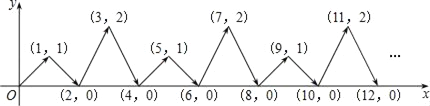
A. (2016,1) B. (2016,0) C. (2016,2) D. (2017,0)
相关试题

