【题目】如图,小明的爸爸去参加一个重要会议,小明坐在汽车上用所学知识绘制了一张反映小车速度与时间的关系图,第二天,小明拿着这张图给同学看,并向同学提出如下问题,你能回答吗?

(1)在上述变化过程中,图象表示了那两个变量的关系?哪个是自变量?哪个是因变量?
(2)小车共行驶了多少时间?最高时速是什么?停止了几分钟?
(3)小车在哪段时间保持匀速行驶?匀速行驶了多少千米?
参考答案:
【答案】(1)图像表示时间和速度的的关系,时间是自变量,速度是因变量;(2)小车共行驶了55分钟,最高时速是85千米/时,停止了5分钟;(3)小车在35分钟到50分钟保持匀速,匀速行驶了21.25千米.
【解析】
(1)根据自变量与因变量的定义求解;
(2)根据速度与时间的图象来求解;
(3)根据速度与时间的图象来求解.
解:(1)图象横坐标是时间,纵坐标是速度,所以图像表示时间和速度的的关系,而速度是随着时间在变化,所以时间是自变量,速度是因变量;
(2)根据图像可知小车共行驶了60-(30-25)=55分钟,最高时速是85千米/时,停止了30-25=5分钟;
(3)当小车匀速行驶时,速度线应该保持水平,结合图像可知小车在35分钟到50分钟保持匀速,达到85千米/时,则匀速行驶了(50-35)![]() 60
60![]() 85=21.25千米.
85=21.25千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,BC=7cm,CD=5cm,P、Q两点分别从B、C两点同时出发,沿矩形ABCD的边以1cm/s的速度逆时针运动,点P到达点C时两点同时停止运动.当点P的运动时间为_s时,△PQC为等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的图像经过点A(0,2)和B(-1,-4).
的图像经过点A(0,2)和B(-1,-4).
(1)求此函数的解析式;并运用配方法,将此抛物线解析式化为
 的形式;
的形式; (2)写出该抛物线顶点C的坐标,并求出△CAO的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年2月3日至2019年2月20日,“第一届”成都金沙太阳节在金沙遗址博物馆成功举办,用世界文明展览,主题灯展,园林花艺,美食演绎等一系列文化活动,与玛雅这一著名的中美洲文明结下不解之缘,为成都人打造了一个博物馆里的“文化年”.春节当天,小杰于下午
 点乘车从家出发,当天按原路返回.如图,是小杰出行的过程中,他距家的距离
点乘车从家出发,当天按原路返回.如图,是小杰出行的过程中,他距家的距离 (千米)与他离家的时间
(千米)与他离家的时间 (小时)之间的图像.根据图像,完成下面的问题:
(小时)之间的图像.根据图像,完成下面的问题:
(1)小杰家距金沙遗址博物馆 千米,他乘车去金沙遗址博物馆的速度是 千米/小时;
(2)已知晚上
 点时,小杰距家
点时,小杰距家 千米,请通过计算说明他何时才能回到家?
千米,请通过计算说明他何时才能回到家?(3)请直接写出小杰回家过程中
 与
与 的关系式.
的关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行并使直角边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=25米,求旗杆AB的高度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为等边三角形,
为等边三角形, 是
是 边上一点,在
边上一点,在 上取一点
上取一点 ,使
,使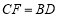 ,在
,在 边上取一点
边上取一点 ,使
,使 ,则
,则 的度数为( )
的度数为( )
A.
 B.
B.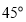 C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的正方形网格中(每个小正方形的边长是1,小正方形的顶点叫作格点),△ABC的顶点均在格点上,请在所给平面直角坐标系中按要求画图和解答下列问题:

(1)以点C为旋转中心,将△ABC绕点C顺时针旋转90°得△CA1B1,画出△CA1B1;
(2)作出△ABC关于点A成中心对称的△AB2C2;
(3)设AC2与y轴交于点D,则△B1DC的面积为_____.
相关试题

