【题目】我们约定:如果身高在选定标准的±2%范围之内都称为“普通身高”.为了了解某校九年级男生中具有“普通身高”的人数,我们从该校九年级男生中随机抽出10名男生,分别测量出他们的身高(单位:cm),收集并整理如下统计表:
根据以上信息,解答如下问题:
(1)计算这组数据的三个统计量:平均数、中位数、众数;
(2)请你分别选择其中一个统计量作为选定标准,找出这10名男生中具有“普通身高”的是哪几位男生?并说明理由.
男生序号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
身高x(cm) | 163 | 171 | 173 | 159 | 161 | 174 | 164 | 166 | 169 | 164 |
参考答案:
【答案】(1)平均数为166.4 cm,中位数为165 cm,众数为164 cm (2)①⑤⑦⑧⑩男生的身高具有“普通身高”. 见解析.
【解析】
(1)根据平均数、中位数、众数的定义进行计算即可得解;
(2)根据(1)中求出的数据,求出普通身高的取值范围,然后确定学生序号即可.
(1)平均数为 ![]() = 166.4 cm;
= 166.4 cm;
10名同学身高从小到大排列如下:
159、161、163、164、164、166、169、171、173、174,
中位数为![]() =165 cm,众数为164 cm.
=165 cm,众数为164 cm.
(2)选平均数作为标准:身高x满足166.4×(1-2%)≤x≤166.4×(1+2%),即163.072≤x≤169.728时为普通身高,此时⑦⑧⑨⑩男生的身高具有“普通身高”;选中位数作为标准:身高x满足165×(1-2%)≤x≤165×(1+2%),即161.7≤x≤168.3时为普通身高,此时①⑦⑧⑩男生的身高具有“普通身高”;选众数作为标准:身高x满足164×(1-2%)≤x≤164×(1+2%),即160.72≤x≤167.28时为普通身高,此时①⑤⑦⑧⑩男生的身高具有“普通身高”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAP+∠APD=180°,∠1=∠2,求证:∠E=∠F.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A被平行直线l1、l2所截,若∠1=100°,∠2=125°,则∠A的度数是( ).
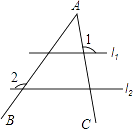
A.25°
B.30°
C.35°
D.45° -
科目: 来源: 题型:
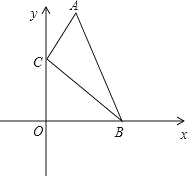
查看答案和解析>>【题目】如图,在直角坐标系中,点A、B的坐标分别为(1,5)和(4,0),点C是y轴上的一个动点,且A、B、C三点不再同一条直线上,当△ABC的周长最小时,点C的坐标是( )
A. (0,1) B. (0,2) C. (0,3) D. (0,4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=8,延长线段AB至C,使得BC=
 AB,延长线段BA至D,使得AD=
AB,延长线段BA至D,使得AD= AB,则下列判断正确的是 ( )
AB,则下列判断正确的是 ( )A. BC=
 AD B. BD=3BC C. BD=4AD D. AC=6AD
AD B. BD=3BC C. BD=4AD D. AC=6AD -
科目: 来源: 题型:
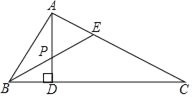
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,∠C=30°,AD⊥BC于D,BE是∠ABC的平分线,且交AD于P,如果AP=2,则AC的长为( )
A. 2 B. 4 C. 6 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )
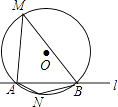
A.2
B.4
C.4
D.8
相关试题

