【题目】如图,在△ABC中,∠A=90°,∠C=30°,AD⊥BC于D,BE是∠ABC的平分线,且交AD于P,如果AP=2,则AC的长为( )
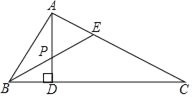
A. 2 B. 4 C. 6 D. 8
参考答案:
【答案】C
【解析】
易得△AEP的等边三角形,则AE=AP=2,在直角△AEB中,利用含30度角的直角三角形的性质来求EB的长度,然后在等腰△BEC中得到CE的长度,则易求AC的长度.
解:∵△ABC中,∠BAC=90°,∠C=30°,
∴∠ABC=60°.
又∵BE是∠ABC的平分线,
∴∠EBC=30°,
∴∠AEB=∠C+∠EBC=60°,∠C=∠EBC,
∴∠AEP=60°,BE=EC.
又AD⊥BC,
∴∠CAD=∠EAP=60°,
则∠AEP=∠EAP=60°,
∴△AEP的等边三角形,则AE=AP=2,
在直角△AEB中,∠ABE=30°,则EB=2AE=4,
∴BE=EC=4,
∴AC=CE+AE=6.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,点A、B的坐标分别为(1,5)和(4,0),点C是y轴上的一个动点,且A、B、C三点不再同一条直线上,当△ABC的周长最小时,点C的坐标是( )
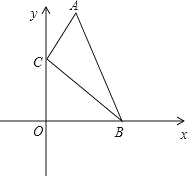
A. (0,1) B. (0,2) C. (0,3) D. (0,4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们约定:如果身高在选定标准的±2%范围之内都称为“普通身高”.为了了解某校九年级男生中具有“普通身高”的人数,我们从该校九年级男生中随机抽出10名男生,分别测量出他们的身高(单位:cm),收集并整理如下统计表:
根据以上信息,解答如下问题:
(1)计算这组数据的三个统计量:平均数、中位数、众数;
(2)请你分别选择其中一个统计量作为选定标准,找出这10名男生中具有“普通身高”的是哪几位男生?并说明理由.
男生序号
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
身高x(cm)
163
171
173
159
161
174
164
166
169
164
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=8,延长线段AB至C,使得BC=
 AB,延长线段BA至D,使得AD=
AB,延长线段BA至D,使得AD= AB,则下列判断正确的是 ( )
AB,则下列判断正确的是 ( )A. BC=
 AD B. BD=3BC C. BD=4AD D. AC=6AD
AD B. BD=3BC C. BD=4AD D. AC=6AD -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )
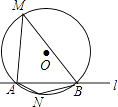
A.2
B.4
C.4
D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5
 cm,且tan∠EFC=0.75,则矩形ABCD的周长为 .
cm,且tan∠EFC=0.75,则矩形ABCD的周长为 . 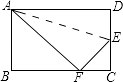
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的顶点坐标是A(﹣7,1),B(1,1),C(1,7).线段DE的端点坐标是D(7,﹣1),E(﹣1,﹣7).
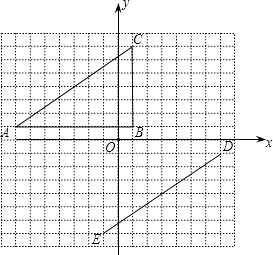
(1)试说明如何平移线段AC,使其与线段ED重合;
(2)将△ABC绕坐标原点O逆时针旋转,使AC的对应边为DE,请直接写出点B的对应点F的坐标;
(3)画出(2)中的△DEF,并和△ABC同时绕坐标原点O逆时针旋转90°,画出旋转后的图形.
相关试题

