Question

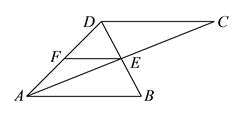
【题目】如图， 平分， 平分， 和交于点， 为的中点，连结．

（）找出图中所有的等腰三角形．

（）若， ，求的长．

Answer 1

【答案】（）所有的等腰三角形有： ， ， ， ;（）．

【解析】试题分析：

（1）由AB∥CD，AC平分∠BAD可得∠C=∠BAC=∠DAC，从而可得AD=CD，得到△ADC是等腰三角形；同理可△ABD是等腰三角形；证∠AED=90°，结合点F是AD中点，可得EF=FD=FA，从而可得△DEF和△AEF是等腰三角形；即图中共有4个等腰三角形；

（2）由∠AED=90°，AE=4，DE=3，由勾股定理可得AD=5，结合点F是AD中点，可得EF=AD=2.5.

试题解析：

（）图中等腰三角形共有4个，分别是： ， ， ， ．理由如下：

∵AB∥CD，AC平分∠BAD，

∴∠C=∠BAC，∠BAC=∠DAC，

∴∠C=∠DAC，

∴AD=CD，

∴△ADC是等腰三角形；

同理可得：△ABD是等腰三角形；

∵BD平分∠ADC，AD=CD，

∴BD⊥AC，

∴∠AED=90°，

又∵点F是AD的中点，

∴EF=AF=DF，

∴△AEF和△DEF是等腰三角形；

综上所述，图中共有四个等腰三角形，分别是：△ADC、△ABD、△AEF和△DEF；

（）∵∠AED=90°，AE=4，DE=3，

∴AD=，

又∵点F是AD的中点，

∴EF=AD=.