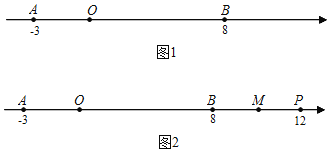
【题目】如果A、B两点在数轴上分别表示有理数a、b,那么它们之间的距离AB=|a﹣b|.如图1,已知数轴上两点A、B对应的数分别为﹣3和8,数轴上另有一个点P对应的数为x
(1)点P、B之间的距离PB= .
(2)若点P在A、B之间,则|x+3|+|x﹣8|= .
(3)①如图2,若点P在点B右侧,且x=12,取BP的中点M,试求2AM﹣AP的值.
②若点P为点B右侧的一个动点,取BP的中点M,那么2AM﹣AP是定值吗?如果是,请求出这个定值;如果不是,请说明理由.
参考答案:
【答案】(1)|8﹣x|;(2)11;(3)①11;②2AM﹣AP是定值,![]() .
.
【解析】
(1)在数轴上A、B两点之间的距离为AB=|a﹣b|,依此即可求解;
(2)根据点P在A、B之间可得﹣3<x<8,然后去绝对值符号求解即可;
(3)①根据中点坐标公式求出点M对应的数,然后列式求2AM﹣AP即可;
②根据中点坐标公式求出点M对应的数,然后列式求2AM﹣AP即可.
解:(1)点P、B之间的距离PB=|8﹣x|,
故答案为:|8﹣x|;
(2)∵点P在A、B之间,
∴﹣3<x<8,
∴|x+3|+|x﹣8|=x+3+8﹣x=11,
故答案为:11;
(3)①∵B对应的数为8,P对应的数为12,点M是BP的中点,
∴M对应的数为![]() =10,
=10,
∴2AM﹣AP=2×(10+3)﹣(12+3)=11;
②设点P对应的数为x,
∵点M是BP的中点,
∴M对应的数为![]() ,
,
∴2AM﹣AP=2×(![]() +3)﹣(x+3)=11,
+3)﹣(x+3)=11,
∴2AM﹣AP是定值,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y1=kx+b(k≠0)与反比例函数y2=
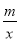 (m≠0)相交于A和B两点,且A点坐标为(1,3),B点的横坐标为﹣3.
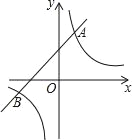
(m≠0)相交于A和B两点,且A点坐标为(1,3),B点的横坐标为﹣3.(1)求反比例函数和一次函数的解析式;
(2)根据图象直接写出使得y1>y2时,x的取值范围.
-
科目: 来源: 题型:
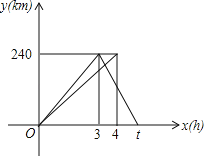
查看答案和解析>>【题目】一辆轿车从甲地驶往乙地,到达乙地后返回甲地,速度是原来的1.5倍,共用t小时;一辆货车同时从甲地驶往乙地,到达乙地后停止.两车同时出发,匀速行驶.设轿车行驶的时间为x(h),两车到甲地的距离为y(km),两车行驶过程中y与x之间的函数图象如图.
(1)求轿车从乙地返回甲地时的速度和t的值;
(2)求轿车从乙地返回甲地时y与x之间的函数关系式,并写出自变量x的取值范围;
(3)直接写出轿车从乙地返回甲地时与货车相遇的时间.
-
科目: 来源: 题型:
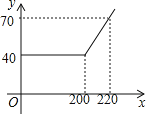
查看答案和解析>>【题目】某网络公司推出了一系列上网包月业务,其中的一项业务是10M“40元包200小时”,且其中每月收取费用y(元)与上网时间x(小时)的函数关系如图所示.
(1)当x≥200时,求y与x之间的函数关系式
(2)若小刚家10月份上网180小时,则他家应付多少元上网费?
(3)若小明家10月份上网费用为52元,则他家该月的上网时间是多少小时?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB,PE与DC交于点O.
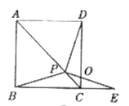
(基础探究)
(1)求证:PD=PE.
(2)求证:∠DPE=90°
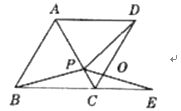
(3)(应用拓展)把正方形ABCD改为菱形,其他条件不变(如图),若PE=3,则PD=________;
若∠ABC=62°,则∠DPE=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市正在开展“食品安全城市”创建活动,为了解学生对食品安全知识的了解情况,学校随机抽取了部分学生进行问卷调查,将调查结果按照“A非常了解、B了解、C了解较少、D不了解”四类分别进行统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:

(1)此次共调查了 名学生;
(2)扇形统计图中D所在扇形的圆心角为 ;
(3)将上面的条形统计图补充完整;
(4)若该校共有800名学生,请你估计对食品安全知识“非常了解”的学生的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数:当x≥0时,它们对应的函数值相等,我们把这样的两个函数称作互为友好函数,例如:一次函数y=x-2,它的友好函数为y=

(1)直接写出一次函数y=-2x+1的友好函数.
(2)已知点A(2,5)在一次函数y=ax-1的友好函数的图象上,求a的值.
(3)已知点B(m,
 )在一次函数y=
)在一次函数y=  x-1的友好函数的图象上,求m的值.
x-1的友好函数的图象上,求m的值.
相关试题

