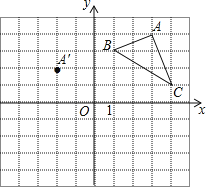
【题目】在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点A′的坐标是(﹣2,2),现将△ABC平移.使点A变换为点A′,点B′、C′分别是B、C的对应点.
(1)请画出平移后的△A′B′C′(不写画法),并直接写出点B′的坐标:B′(_____________);
(2)若△ABC内部一点P的坐标为(a,b),则点P的对应点P′的坐标是(________________);
(3)求出△ABC的面积.
参考答案:
【答案】(1)如图所示见解析;B′(﹣4,1 );(2)点P的对应点P′的坐标是( a﹣5,b﹣2 ); (3)△ABC的面积为3.5.
【解析】
(1)根据平移的作图方法作图后直接写出坐标;
(2)首先根据A与A′的坐标观察变化规律,P的坐标变换与A点的变换一样;
(3)先求出△ABC所在的矩形的面积,然后减去△ABC四周的三角形的面积即可.
(1)如图所示:B′(﹣4,1 )
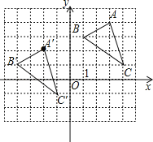
(2)点P的对应点P′的坐标是( a﹣5,b﹣2 );
(3))△ABC的面积为:3×3﹣2×2÷2﹣3×1÷2﹣2×3÷2=3.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是正方形ABCD的边BC延长线上一点,连接DE,过顶点B作BF⊥DE,垂足为F,BF分别交AC于H,交CD于G.
(1)求证:BG=DE;
(2)若点G为CD的中点,求
 的值;
的值;(3)在(2)的条件下,求
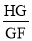 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题的提出:
如果点P是锐角△ABC内一动点,如何确定一个位置,使点P到△ABC的三顶点的距离之和PA+PB+PC的值为最小?
问题的转化:
(1)把ΔAPC绕点A逆时针旋转60度得到
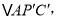 连接
连接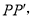 这样就把确定PA+PB+PC的最小值的问题转化成确定
这样就把确定PA+PB+PC的最小值的问题转化成确定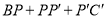 的最小值的问题了,请你利用如图证明:
的最小值的问题了,请你利用如图证明: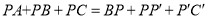 ;
;问题的解决:
(2)当点P到锐角△ABC的三项点的距离之和PA+PB+PC的值为最小时,请你用一定的数量关系刻画此时的点P的位置:_____________________________;
问题的延伸:
(3)如图是有一个锐角为30°的直角三角形,如果斜边为2,点P是这个三角形内一动点,请你利用以上方法,求点P到这个三角形各顶点的距离之和的最小值.
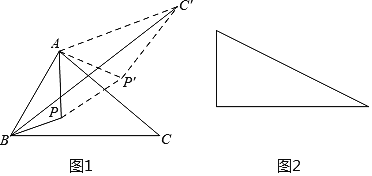
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2018次相遇地点的坐标是( )

A. (1,﹣1) B. (2,0) C. (﹣1,1) D. (﹣1,﹣1)
-
科目: 来源: 题型:
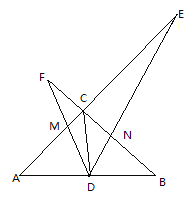
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为E、F,DF与AC交于点M,DE与BC交于点N。
(1)求证:△ADM∽△BND;
(2)在∠EDF绕点D旋转的过程中:
①探究三条线段CD、CE、CF之间的数量关系,并说明理由;
②若CE=4,CF=2,求DN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c交x轴于(﹣1,0)、(3,0)两点,以下四个结论正确的是(用序号表示)______________.
(1)图象的对称轴是直线 x=1
(2)当x>1时,y随x的增大而减小
(3)一元二次方程ax2+bx+c=0的两个根是﹣1和3
(4)当﹣1<x<3时,y<0.
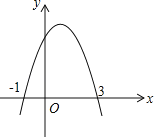
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个口袋中装有3个白球、5个红球,这些球除了颜色外完全相同,充分摇匀后随机摸出一球,
(1)求摸出白球概率是多少?
(2)在第一次摸出白球后,如果将这个白球放回,再摸出一球,求两次摸出的都是白球的概率是多少?(用树状图或列表分析)
相关试题

