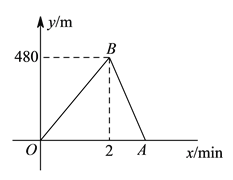
【题目】小明和小敏进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的![]() 倍.设两人出发
倍.设两人出发![]() 后距出发点的距离为ym.图中折线段
后距出发点的距离为ym.图中折线段![]() 表示小明在整个训练中y与x的函数关系.
表示小明在整个训练中y与x的函数关系.
(![]() )点
)点![]() 所表示的实际意义是__________.
所表示的实际意义是__________.
(![]() )求
)求![]() 所在直线的函数表达式.
所在直线的函数表达式.
(![]() )如果小敏上坡平均速度是小明上坡平均速度的一半,那么两人出发后多长时间第一次相遇?
)如果小敏上坡平均速度是小明上坡平均速度的一半,那么两人出发后多长时间第一次相遇?
参考答案:
【答案】(1)小明出发2分钟跑到坡顶,此时离坡脚480米;
(![]() )AB所在直线的函数表达式为
)AB所在直线的函数表达式为![]() ;
;
(![]() )两人第一次相遇时间为
)两人第一次相遇时间为![]() .
.
【解析】试题分析:(1)根据到出发点的距离由大变小可知小亮2min时开始下坡返回;(2)求出下坡时的速度,然后求出下坡的时间,从而得到点A的坐标,设直线AB的解析式为y=kx+b,利用待定系数法求一次函数解析式解答;(3)设两人出发后xmin相遇,根据第一次相遇时,小敏下坡,小明上坡,列出方程求解即可.
试题解析:(![]() )小明出发
)小明出发![]() 分钟跑到坡顶,此时离坡脚
分钟跑到坡顶,此时离坡脚![]() 米.
米.
(![]() )小明上坡的平均速度为
)小明上坡的平均速度为 ![]() ,
,
则其下坡的平均速度为 ![]() ,
,
故回到出发点时间为 ![]() .
.
所以![]() 点坐标为
点坐标为![]() ,
,
设![]() 所在直线的函数表达式为
所在直线的函数表达式为![]() ,
,
因为![]() 的图像过点
的图像过点![]() 、
、![]() ,
,
所以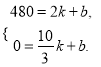
解方程组,得![]()
所以![]() 所在直线的函数表达式为
所在直线的函数表达式为![]() .
.
(![]() )根据题意,可知小敏上坡的平均速度为
)根据题意,可知小敏上坡的平均速度为![]() ,
,
设小敏出发![]() 后距出发点的距离为
后距出发点的距离为![]() ,
,
所以![]() ,解方程组
,解方程组![]() 得
得![]()
因此,两人第一次相遇时间为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:①内错角相等;②面积相等的两个三角形全等;③钝角三角形的三条高线所在直线的交点在三角形内; ④等腰三角形两底角的平分线相等。其中真命题是( )
A. ① B. ② C. ③ D. ④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的分式方程
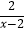 +
+ 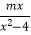 =
= 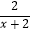 .
.
(1)若方程的增根为x=2,求m的值;
(2)若方程有增根,求m的值;
(3)若方程无解,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个凸六边形的六个内角都是120°,六条边的长分别为a,b,c,d,e,f,则下列等式中成立的是( )
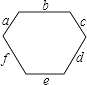
A.a+b+c=d+e+f
B.a+c+e=b+d+f
C.a+b=d+e
D.a+c=b+d -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a+b=5,ab=-6,求:(1)a2b+ab2的值;(2)a2+b2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=2(x+1)2﹣3的顶点坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(m﹣1,2m+1)在第一象限,则m的取值范围是 .
相关试题

