【题目】观察下列等式:
第1个等式:a1=![]()
![]() ×(1﹣
×(1﹣![]() );
);
第2个等式:a2=![]() ;
;
第3个等式:a3=![]() ;
;
第4个等式:a4=![]() ;
;
…
请解答下列问题:
(1)按以上规律列出第5个等式:a5= ;
(2)用含有n的代数式表示第n个等式:an= = (n为正整数);
(3)若![]() 的值为
的值为![]() ,求n的值.
,求n的值.
参考答案:
【答案】⑴![]() ; ⑵
; ⑵![]() ;⑶
;⑶![]()
【解析】
(1)(2)由题意可知:分子为1,分母是两个连续奇数的乘积,可以拆成:分子是1,分母是以这两个连续奇数为分母的两个分数的差的![]() ,由此得出第5个等式以及第n个等式;
,由此得出第5个等式以及第n个等式;
(3)运用以上规律,采用拆项相消法即可解决问题.
解:(1)按以上规律可得,第5个等式:a5=![]() ;
;
(2)按以上规律可得,第n个等式:an=![]() (n为正整数);
(n为正整数);
⑶原式=![]() ×(1-
×(1-![]() )+
)+![]() ×(
×(![]() -
-![]() )+
)+![]() ×(
×(![]() -
-![]() )+…+
)+…+![]() (
(![]() )
)
=![]() ,
,
解得 ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线
 与X轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连接AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动,线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒).
与X轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连接AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动,线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒).
(1)求A,B,C三点的坐标和抛物线的顶点的坐标;
(2)当t为何值时,四边形PQCA为平行四边形?请写出计算过程;
(3)当
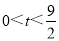 时,△PQF的面积是否总为定值?若是,求出此定值,若不是,请说明理由;
时,△PQF的面积是否总为定值?若是,求出此定值,若不是,请说明理由;(4)当t为何值时,△PQF为等腰三角形?请写出解答过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
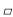 ABCD中,点E为CD的中点,点F在BC上,且CF=2BF,连接AE,AF,若AF=
ABCD中,点E为CD的中点,点F在BC上,且CF=2BF,连接AE,AF,若AF=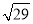 ,AE=7,tan∠EAF=
,AE=7,tan∠EAF=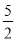 ,则线段BF的长为__________.
,则线段BF的长为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,D、E分别是BC、AC中点,BF平分∠ABC.交DE于点F.AB=8,BC=6,则EF的长为( )
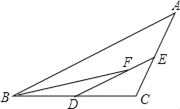
A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,随着我国科学技术的迅猛发展,很多行业已经由“中国制造”升级为“中国创造”,高铁事业是“中国创造”的典范,甲、乙两个城市的火车站相距1280千米,加开高铁后,从甲站到乙站的运行时间缩短了11个小时,大大方便了人们出行,已知高铁行驶速度是原来火车速度的3.2倍,求高铁的行驶速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某景区的水上乐园有一批
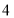 人座的自划船,每艘可供
人座的自划船,每艘可供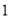 至
至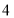 位游客乘坐游湖,因景区加大宣传,预计今年游客将会增加.水上乐园的工作人员在去年
位游客乘坐游湖,因景区加大宣传,预计今年游客将会增加.水上乐园的工作人员在去年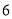 月
月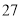 日一天出租的
日一天出租的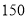 艘次
艘次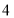 人自划船中随机抽取了
人自划船中随机抽取了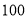 艘,对其中抽取的每艘船的乘坐人数进行统计,并制成如下统计图.
艘,对其中抽取的每艘船的乘坐人数进行统计,并制成如下统计图.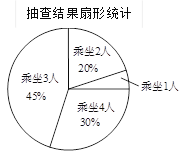
(1)求扇形统计图中, “乘坐1人”所对应的圆心角度数;
(2)估计去年
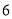 月
月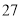 日这天出租的
日这天出租的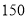 艘次
艘次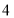 人自划船平均每艘船的乘坐人数;
人自划船平均每艘船的乘坐人数;(3)据旅游局预报今年
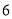 月
月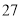 日这天该景区可能将增加游客300人,请你为景区预计这天需安排多少艘4人座的自划船才能满足需求.
日这天该景区可能将增加游客300人,请你为景区预计这天需安排多少艘4人座的自划船才能满足需求. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:如图,点A、B在数轴上分别表示有理数a、b,则A、B两点之间的距离可以表示为|a﹣b|.
根据阅读材料与你的理解回答下列问题:
(1)数轴上表示3与﹣2的两点之间的距离是 .
(2)数轴上有理数x与有理数7所对应两点之间的距离用绝对值符号可以表示为 .
(3)代数式|x+8|可以表示数轴上有理数x与有理数 所对应的两点之间的距离;若|x+8|=5,则x= .
(4)求代数式|x+1008|+|x+504|+|x﹣1007|的最小值.

相关试题

