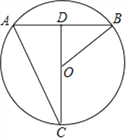
【题目】如图,点C在⊙O上,连接CO并延长交弦AB于点D,![]() ,连接AC、OB,若CD=40,AC=
,连接AC、OB,若CD=40,AC=![]() .
.
(1)求弦AB的长;
(2)求sin∠ABO的值.
参考答案:
【答案】(1)0(2)![]()
【解析】分析:
(1)由CD过圆心O,![]() 可得CD⊥AB,AB=2AD=2BD,结合CD=40,AC=
可得CD⊥AB,AB=2AD=2BD,结合CD=40,AC=![]() 由勾股定理可得AD=20,由此可得AB=2AD=40;
由勾股定理可得AD=20,由此可得AB=2AD=40;
(2)设⊙O的半径为r,在Rt△BDO中由勾股定理建立关于r的方程,解方程求得r的值,即可在Rt△BDO中,由sin∠ABO=![]() 求得sin∠ABO的值.
求得sin∠ABO的值.
详解:
(1)∵CD过圆心O,![]() ,
,
∴CD⊥AB,AB=2AD=2BD,
∴∠ADC=90°,
又∵CD=40,AC=![]() ,
,
∴AD=![]() ,
,
∴AB=2AD=40;
(2)设圆O的半径为r,则OD=CD-OC=40-r,、
∵BD=AD=20,∠ODB=90°,
∴BD2+OD2=OB2,
∴![]() ,
,
解得:![]() ,
,
∴DO=40-25=15,
∴sin∠ABO=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用如图4×4方格,每个小正方形的边长都为
 .
.
(1)请求出图1中阴影正方形的面积与边长;
(2)请在图2中画出一个与图1中阴影部分面积不相等的正方形,要求它的边长为无理数,并求出它的边长;
(3)把分别表示图1与图2中的正方形的边长的实数在数轴上表示出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠AFC=______度;
(2)求∠EDF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AE、DE分别平分∠BAD、∠ADC,E点在BC上.
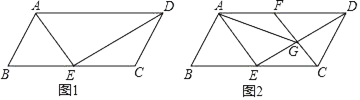
(1)求证:BC=2AB;
(2)若AB=3cm,∠B=60°,一动点F以1cm/s的速度从A点出发,沿线段AD运动,CF交DE于G,当CF∥AE时:
①求点F的运动时间t的值;②求线段AG的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】星期天天气晴好,小米骑自行车向宁波登山基地九峰山出发,由于太匆忙,出发半个小时后,他爸爸发现他把可以免费进入景区的证件落在家里,于是,他立即开摩托车去追,已知小米骑自行车的平均速度为
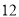 千米/时,摩托车的平均速度为
千米/时,摩托车的平均速度为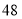 千米/时.
千米/时.(1)求出爸爸多长时间能追上小米?
(2)若爸爸出发的同时手机通知小米掉头回来,那么爸爸多久与小米相遇?
(3)若爸爸出发的同时手机通知小米掉头来取,结果爸爸出发十分钟还没有遇到小米,手机联系才发现他俩已经错开了一段距离了,这时他们又赶紧掉头,问爸爸从家里出发到送证件成功共花了多少时间?
(4)小米继续骑自行车,他留意到每隔
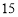 分钟有一辆某路公交车从他身后驶向前面,假设小米的平均速度是
分钟有一辆某路公交车从他身后驶向前面,假设小米的平均速度是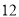 千米/时,公交车的的平均速度为
千米/时,公交车的的平均速度为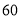 千米/时.小米就想:每隔几分钟从车站开出一辆该路公交车呢?请你帮小米求岀.
千米/时.小米就想:每隔几分钟从车站开出一辆该路公交车呢?请你帮小米求岀. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵5元,用360元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.
(1)求甲、乙两种商品每件的价格各是多少元?
(2)若商店计划购买这两种商品共40件,且投入的经费不超过1150元,那么,最多可购买多少件甲种商品?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为响应推进中小学生素质教育的号召,某校决定在下午15点至16点开设以下选修课:音乐史、管乐、篮球、健美操、油画.为了解同学们的选课情况,某班数学兴趣小组从全校三个年级中各调查一个班级,根据相关数据,绘制如下统计图.

(1)请根据以上信息,直接补全条形统计图(图1)和扇形统计图(图2);
(2)若初一年级有180人,请估算初一年级中有多少学生选修音乐史?
(3)若该校共有学生540人,请估算全校有多少学生选修篮球课?
相关试题

