【题目】利用如图4×4方格,每个小正方形的边长都为![]() .
.

(1)请求出图1中阴影正方形的面积与边长;
(2)请在图2中画出一个与图1中阴影部分面积不相等的正方形,要求它的边长为无理数,并求出它的边长;
(3)把分别表示图1与图2中的正方形的边长的实数在数轴上表示出来.
参考答案:
【答案】(1)面积为10,边长为![]() ;(2)见解析,
;(2)见解析,![]() ;(3)见解析
;(3)见解析
【解析】
(1)先用割补法求出阴影正方形的面积,进而求出阴影正方形的边长,即可;
(2)类似第(1)题,作出正方形,再求出面积,进而求出边长,即可;
(3)用圆规把分别表示图1与图2中的正方形的边长截取出来,进而即可把它们对应的实数在数轴上表示出来.
(1)4×4-4×![]() ×1×3=10,10的算术平方根为
×1×3=10,10的算术平方根为![]() ,
,
答:阴影正方形的面积为10,边长为![]() ;
;
(2)如图所示:

∵3×3-4×![]() ×1×2=5,5的算术平方根为
×1×2=5,5的算术平方根为![]() ,
,
∴正方形的边长为:![]() ;
;
(3)如图所示:

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,两个全等的Rt△AOB、Rt△OCD分别位于第二、第一象限,∠ABO=∠ODC=90°,OB、OD在x轴上,且∠AOB=30°,AB=1.
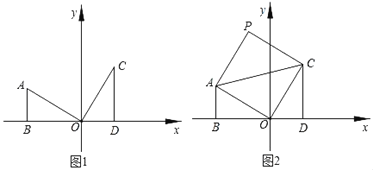
(1)如图1中Rt△OCD可以看作由Rt△AOB先绕点O顺时针旋转 度,再绕斜边中点旋转 度得到的,C点的坐标是 ;
(2)是否存在点E,使得以C、O、D、E为顶点的四边形是平行四边形,若存在,写出E点的坐标;若不存在请说明理由.
(3)如图2将△AOC沿AC翻折,O点的对应点落在P点处,求P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蔬菜店第一次用800元购进某种蔬菜,由于销售状况良好,该店又用1400元第二次购进该品种蔬
菜,所购数量是第一次购进数量的2倍,但进货价每千克少了0.5元.
(1)第一次所购该蔬菜的进货价是每千克多少元?
(2)蔬菜店在销售中,如果两次售价均相同,第一次购进的蔬菜有3% 的损耗,第二次购进的蔬菜有5% 的损耗,若该蔬菜店售完这些蔬菜获利不低于1244元,则该蔬菜每千克售价至少为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线, AF⊥BE , 垂足为P.像△ABC这样的三角形均为“中垂三角形”.设
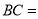
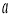 ,
, ,
,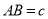 .
.
特例探索
(1)如图1,当∠
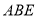 =45°,
=45°,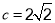 时,
时,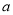 = ,
= ,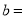 ;
;如图2,当∠
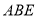 =30°,
=30°,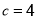 时,
时, 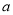 = ,
= ,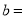 ;
;归纳证明
(2)请你观察(1)中的计算结果,猜想
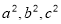 三者之间的关系,用等式表示出来,
三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式;
拓展应用
(3)如图4,在□ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG, AD=
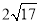 ,AB=6.
,AB=6.求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是BC边上的一点,∠B=50°,∠BAD=30°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠AFC=______度;
(2)求∠EDF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AE、DE分别平分∠BAD、∠ADC,E点在BC上.
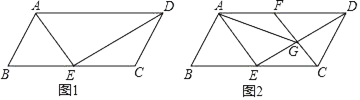
(1)求证:BC=2AB;
(2)若AB=3cm,∠B=60°,一动点F以1cm/s的速度从A点出发,沿线段AD运动,CF交DE于G,当CF∥AE时:
①求点F的运动时间t的值;②求线段AG的长度.
-
科目: 来源: 题型:
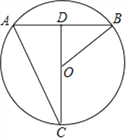
查看答案和解析>>【题目】如图,点C在⊙O上,连接CO并延长交弦AB于点D,
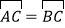 ,连接AC、OB,若CD=40,AC=
,连接AC、OB,若CD=40,AC=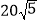 .
.(1)求弦AB的长;
(2)求sin∠ABO的值.
相关试题

