【题目】已知:如图,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE,CF.
(1)求证:AF=CE;
(2)若AC=EF,试判断四边形AFCE是什么样的四边形,并证明你的结论.
参考答案:
【答案】
(1)证明:在△ADF和△CDE中,
∵AF∥BE,
∴∠FAD=∠ECD.
又∵D是AC的中点,
∴AD=CD.
∵∠ADF=∠CDE,
∴△ADF≌△CDE.
∴AF=CE.
(2)解:若AC=EF,则四边形AFCE是矩形.
证明:由(1)知:AF=CE,AF∥CE,
∴四边形AFCE是平行四边形.
又∵AC=EF,
∴平行四边形AFCE是矩形
【解析】(1)证线段AF=CE,可证它们所在的三角形全等,即△ADF≌△CDE;(2)利用(1)的结论易证四边形AFCE是平行四边形,再加上对角线相等,可得四边形AFCE是矩形.
【考点精析】关于本题考查的矩形的判定方法,需要了解有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中考体考临近,某校计划让九年级10个班的480名学生在“立定跳远”、“掷实心球”、“跳绳”三个项目中选择一项进行针对性强化训练.为了提前了解全年级总体情况,小明从每个班中随机抽取5名学生进行问卷调查,并将统计结果制成如下两幅不完整的统计表和统计图.


(1)请将统计表、统计图补充完整;
(2)请以小明的统计结果来估算该校九年级480名学生参加“跳绳”训练的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个几何体的主视图和左视图都是底边长为6,高为4的等腰三角形,俯视图是一个圆,那么这个几何体的侧面积是( )

A.12π
B.24π
C. π
π
D.15π -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的两边长分别为5和7,则第三边的中线长x的取值范围是( )
A.
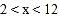 B.
B.  C.
C.  D. 无法确定
D. 无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
 ,点
,点 ,
, 分别在
分别在 ,
, 上,
上, 射线
射线 绕
绕 点顺时针旋转至
点顺时针旋转至 便立即逆时针回转,射线
便立即逆时针回转,射线 绕
绕 点顺时针旋转至
点顺时针旋转至 便立即逆时针回转.射线
便立即逆时针回转.射线 转动的速度是每秒
转动的速度是每秒 度,射线
度,射线 转动的速度是每秒
转动的速度是每秒 度.
度.
(1)直接写出
 的大小为_______;
的大小为_______;(2)射线
 、
、 转动后对应的射线分别为
转动后对应的射线分别为 、
、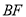 ,射线
,射线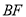 交直线
交直线 于点
于点 ,若射线
,若射线 比射线
比射线 先转动
先转动 秒,设射线
秒,设射线 转动的时间为
转动的时间为
 秒,求
秒,求 为多少时,直线
为多少时,直线 直线
直线 ?
?(3)如图2,若射线
 、
、 同时转动
同时转动
 秒,转动的两条射线交于点
秒,转动的两条射线交于点 ,作
,作 ,点
,点 在
在 上,请探究
上,请探究 与
与 的数量关系.
的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连结CQ.若PA∶PB∶PC=3∶4∶5,连结PQ,试判断△PQC的形状( )

A. 直角三角形 B. 等腰三角形 C. 锐角三角形 D. 钝角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠BOP与OP上点C,点A(在点C的右边),李玲现进行如下操作:①以点O为圆心,OC长为半径画弧,交OB于点D,连接CD;②以点A为圆心,OC长为半径画弧MN,交OA于点M;③以点M为圆心,CD长为半径画弧,交弧MN于点E,连接ME,操作结果如图所示,下列结论不能由上述操作结果得出的是( )

A. CD∥ME B. OB∥AE C. ∠ODC=∠AEM D. ∠ACD=∠EAP
相关试题

