搜索
【题目】如图，正方形网格中，小正方形的边长为1，△ABC的顶点在格点上．
（1）判断△ABC是否是直角三角形？并说明理由．
（2）求△ABC的面积．
参考答案：
【答案】（1）△ABC是直角三角形，理由详见解析；（2）13.
【解析】
（1）根据勾股定理求得△ABC各边的长，再利用勾股定理的逆定理进行判定其形状即可；（2）利用经过△ABC三个顶点的长方形的面积减去以点A、B、C为直角顶点的三个直角三角形的面积求解即可.
（1）△ABC是直角三角形，理由如下：
由勾股定理可得：AC2=32+22=13，BC2=82+12=65，AB2=62+42=52，
∴AB2+AC2=BC2，
∴△ABC是直角三角形；
（2）S△ABC=8×4﹣
×2×3﹣×8×1﹣×4×6=13．
-
科目： 来源： 题型：
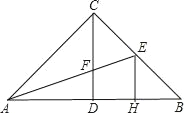
查看答案和解析>>【题目】如图，在△ABC中，∠ACB=90°，高CD和角平分线AE交于点F，EH⊥AB于点H，那么CF=EH吗？说明理由．
-
科目： 来源： 题型：
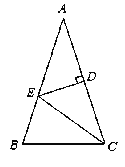
查看答案和解析>>【题目】如图， △ABC中，AB=AC，∠A=36°，AC的垂直平分线交AB于E，D为垂足，连结EC
⑴求∠ECD的度数；
⑵若CE=5，求CB的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校部分团员参加社会公益活动，准备购进一批许愿瓶进行销售，并将所得利润捐助给慈善机构．根据市场调查，这种许愿瓶一段时间内的销售量y （单位：个）与销售单价x（单位：元/个）之间的对应关系如图所示：
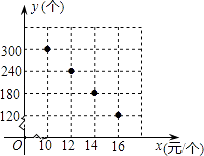
（1）y与x之间的函数关系是 ．
（2）若许愿瓶的进价为6元/个，按照上述市场调查的销售规律，求销售利润w（单位：元）与销售单价x （单位：元/个）之间的函数关系式；
（3）在（2）问的条件下，若许愿瓶的进货成本不超过900元，要想获得最大利润，试确定这种许愿瓶的销售单价，并求出此时的最大利润． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=﹣
x2+bx+c与x轴交于A，B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（﹣1，0），C（0，2）．
（1）求抛物线的解析式；
（2）在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由；
（3）点E时线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，△CBF的面积最大？求出△CBF的最大面积及此时E点的坐标． -
科目： 来源： 题型：
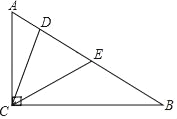
查看答案和解析>>【题目】如图，在△ACB中，∠ACB=90°，D、E为斜边AB上的两点，且BD=BC，AE=AC，求∠DCE的度数．
-
科目： 来源： 题型：
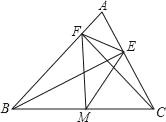
查看答案和解析>>【题目】如图，在△ABC中，CF⊥AB于F，BE⊥AC于E，M为BC的中点．
（1）若EF=3，BC=8，求△EFM的周长；
（2）若∠ABC=50°，∠ACB=60°，求∠EMF的度数．
相关试题
