【题目】如图,抛物线y=﹣ ![]() x2+bx+c与x轴交于A,B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+bx+c与x轴交于A,B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,△CBF的面积最大?求出△CBF的最大面积及此时E点的坐标.
参考答案:
【答案】
(1)
解:把A(﹣1,0),C(0,2)代入y=﹣ ![]() x2+bx+c得
x2+bx+c得 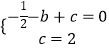 ,
,
解得 ![]() ,c=2,
,c=2,
∴抛物线的解析式为y=﹣ ![]() x2+
x2+ ![]() x+2
x+2
(2)
解:存在.如图1中,∵C(0,2),D( ![]() ,0),
,0),
∴OC=2,OD= ![]() ,CD=
,CD= ![]() =
= ![]()
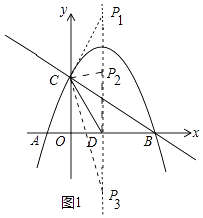
①当CP=CD时,可得P1( ![]() ,4).
,4).
②当DC=DP时,可得P2( ![]() ,
, ![]() ),P3(
),P3( ![]() ,﹣
,﹣ ![]() )
)
综上所述,满足条件的P点的坐标为 ![]() 或
或 ![]() 或
或 ![]()
(3)
解:如图2中,
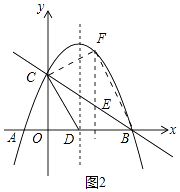
对于抛物线y=﹣ ![]() x2+
x2+ ![]() x+2,当y=0时,﹣
x+2,当y=0时,﹣ ![]() x2+
x2+ ![]() x+2=0,解得x1=4,x2=﹣1
x+2=0,解得x1=4,x2=﹣1
∴B(4,0),A(﹣1,0),
由B(4,0),C(0,2)得直线BC的解析式为y=﹣ ![]() x+2,
x+2,
设E ![]() 则F
则F ![]() ,
,
EF= ![]() ﹣
﹣ ![]() =
= ![]()
∴- ![]() <0,∴当m=2时,EF有最大值2,
<0,∴当m=2时,EF有最大值2,
此时E是BC中点,
∴当E运动到BC的中点时,△EBC面积最大,
∴△EBC最大面积= ![]() ×4×EF=
×4×EF= ![]() ×4×2=4,此时E(2,1)
×4×2=4,此时E(2,1)
【解析】(1)把A(﹣1,0),C(0,2)代入y=﹣ ![]() x2+bx+c列方程组即可.(2)先求出CD的长,分两种情形①当CP=CD时,②当DC=DP时分别求解即可.(3)求出直线BC的解析式,设E
x2+bx+c列方程组即可.(2)先求出CD的长,分两种情形①当CP=CD时,②当DC=DP时分别求解即可.(3)求出直线BC的解析式,设E ![]() 则F
则F ![]() ,构建二次函数,利用二次函数的性质即可解决问题.
,构建二次函数,利用二次函数的性质即可解决问题.
【考点精析】关于本题考查的二次函数的图象和二次函数的性质,需要了解二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.
-
科目: 来源: 题型:
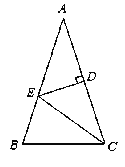
查看答案和解析>>【题目】如图, △ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连结EC
⑴求∠ECD的度数;
⑵若CE=5,求CB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y (单位:个)与销售单价x(单位:元/个)之间的对应关系如图所示:
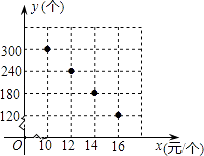
(1)y与x之间的函数关系是 .
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(单位:元)与销售单价x (单位:元/个)之间的函数关系式;
(3)在(2)问的条件下,若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中,小正方形的边长为1,△ABC的顶点在格点上.
(1)判断△ABC是否是直角三角形?并说明理由.
(2)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ACB中,∠ACB=90°,D、E为斜边AB上的两点,且BD=BC,AE=AC,求∠DCE的度数.
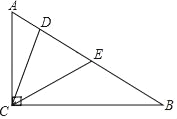
-
科目: 来源: 题型:
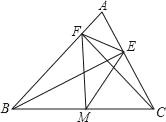
查看答案和解析>>【题目】如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.
(1)若EF=3,BC=8,求△EFM的周长;
(2)若∠ABC=50°,∠ACB=60°,求∠EMF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.

(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:BE+CF= AB.
AB.
(3)如图3,若∠EDF的两边分别交AB,AC的延长线于E、F两点,(2)中的结论还成立吗?如果成立,请证明;如果不成立,请直接写出线段BE,AB,CF之间的数量关系.
相关试题

