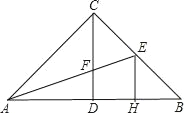
【题目】如图,在△ABC中,∠ACB=90°,高CD和角平分线AE交于点F,EH⊥AB于点H,那么CF=EH吗?说明理由.
参考答案:
【答案】详见解析.
【解析】
根据角平分线的性质得出CE=HE,∠CAE=∠EAH,再由两角互补的性质得出∠AEC=∠AEH,根据平行线的性质得出∠EFC=∠AEH,所以∠AEC=∠EFC,即可证得结论.
∵在△ABC中,∠ACB=90°,高CD和角平分线AE交于点F,EH⊥AB于点H,
∴CE=HE,∠CAE=∠EAH,
∵∠CAE+∠AEC=90°,∠EAH+∠AEF=90°
∴∠AEC=∠AEH,
∵CD⊥AB,EH⊥AB,
∴CD∥EH,
∴∠EFC=∠AEH,
∴∠AEC=∠EFC,
∴CE=CF,
∴CF=EH.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是正方形,△ABC的顶点均在格点上,建立平面直角坐标系.
(1)以原点O为对称中心,画出与△ABC关于原点O对称的△A1B1C1 , A1的坐标是
(2)将原来的△ABC绕着点(﹣2,1)顺时针旋转90°得到△A2B2C2 , 试在图上画出△A2B2C2的图形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=10,则S2的值是_________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC; ②∠BCE+∠BCD=180°; ③AF2=EC2﹣EF2; ④BA+BC=2BF.其中正确的是_____.

-
科目: 来源: 题型:
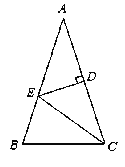
查看答案和解析>>【题目】如图, △ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连结EC
⑴求∠ECD的度数;
⑵若CE=5,求CB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y (单位:个)与销售单价x(单位:元/个)之间的对应关系如图所示:
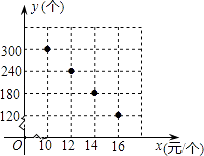
(1)y与x之间的函数关系是 .
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(单位:元)与销售单价x (单位:元/个)之间的函数关系式;
(3)在(2)问的条件下,若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中,小正方形的边长为1,△ABC的顶点在格点上.
(1)判断△ABC是否是直角三角形?并说明理由.
(2)求△ABC的面积.

相关试题

