【题目】(1)如图(1),已知:在等腰直角三角形![]() 中,
中,![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() 直线
直线![]() ,
,![]() 直线
直线![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() .则
.则![]() 、
、![]() 和
和![]() 之间的数量关系是: .
之间的数量关系是: .
(2)如图(2),将(1)中的条件改为:在等腰三角形![]() 中,
中,![]() 、
、![]() 、
、![]() 三点都在直线
三点都在直线![]() 上,且
上,且![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论
为任意锐角或钝角.请问结论![]() 是否成立?如成立,请你给出证明;若不成立,请说明理由.
是否成立?如成立,请你给出证明;若不成立,请说明理由.
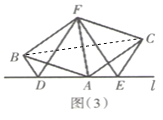
(3)拓展与应用:如图(3),![]() 、
、![]() 是直线
是直线![]() 上的两动点(
上的两动点(![]() 、
、![]() 、
、![]() 三点互不重合),点
三点互不重合),点![]() 为
为![]() 平分线上的一点,且
平分线上的一点,且![]() 和
和![]() 均为等边三角形,连接
均为等边三角形,连接![]() 、
、![]() ,若
,若![]() ,求证:
,求证:![]() .
.

参考答案:
【答案】(1)DE=BD+CE;(2)成立;(3)理由见解析.
【解析】
(1)根据同角的余角相等得出∠CAE=∠ABD,进而利用AAS得出△ABD≌△CAE,即可得出DE=BD+CE;
(2)根据∠BDA=∠AEC=∠BAC=α,得出∠CAE=∠ABD.在△ADB和△CEA中,根据AAS证出△ADB≌△CEA,从而得出AE=BD,AD=CE,即可证出DE=BD+CE;
(3)连接BC.由(2)的结论得到△ADB≌△CEA,则BD=AE,∠DBA=∠CAE,根据等边三角形的性质得∠ABF=∠CAF=60°,则有∠DBF=∠FAE,利用“SAS”可证明△DBF≌△EAF,即可得出结论.
(1)DE=BD+CE.理由如下:
如图1.
∵BD⊥l,CE⊥l,∴∠BDA=∠AEC=90°.
又∵∠BAC=90°,∴∠BAD+∠CAE=90°,∠BAD+∠ABD=90°,∴∠CAE=∠ABD.
在△ABD和△CAE中,∵ ,∴△ABD≌△CAE(AAS),∴BD=AE,AD=CE.
,∴△ABD≌△CAE(AAS),∴BD=AE,AD=CE.
∵DE=AD+AE,∴DE=CE+BD;
(2)成立.理由如下:
如图2.
∵∠BDA=∠AEC=∠BAC=α,∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,∴∠CAE=∠ABD.
在△ADB和△CEA中,∵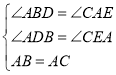 ,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴BD+CE=AE+AD=DE;
,∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴BD+CE=AE+AD=DE;
(3)DF=EF.理由如下:
连接BC.
∵△ABF和△ACF均为等边三角形,∴BF=BA=AF=AC,∠ABF=∠CAF=60°.
由(2)知,△ADB≌△CAE,BD=EA,∠DBA=∠CAE.
∵∠ABF=∠CAF=60°,∴∠DBA+∠ABF=∠CAE+∠CAF,∴∠DBF=∠FAE.
在△DBF和△EAF中,∵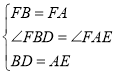 ,∴△DBF≌△EAF(SAS),∴DF=EF.
,∴△DBF≌△EAF(SAS),∴DF=EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明站在池塘边的
 点处,池塘的对面(小明的正北方向)
点处,池塘的对面(小明的正北方向) 处有一棵小树,他想知道这棵树距离他有多远,于是他向正东方向走了12步到达电线杆
处有一棵小树,他想知道这棵树距离他有多远,于是他向正东方向走了12步到达电线杆 旁,接着再往前走了12步,到达
旁,接着再往前走了12步,到达 处,然后他改向正南方向继续行走,当小明看到电线杆
处,然后他改向正南方向继续行走,当小明看到电线杆 、小树
、小树 与自己现处的位置
与自己现处的位置 在一条直线上时,他共走了60步.
在一条直线上时,他共走了60步.(1)根据题意,画出示意图(写出作图步骤);
(2)如果小明一步大约40
 ,估算出小明在点
,估算出小明在点 处时小树与他的距离为多少米,并说明理由.
处时小树与他的距离为多少米,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某篮球运动员去年共参加40场比赛,其中3分球的命中率为0.25,平均每场有12次3分球未投中.
(1)该运动员去年的比赛中共投中多少个3分球?
(2)在其中的一场比赛中,该运动员3分球共出手20次,小亮说,该运动员这场比赛中一定投中了5个3分球,你认为小亮的说法正确吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 和
和 都是等腰三角形,
都是等腰三角形, ,
, ,
, .
.(初步感知)(1)特殊情形:如图①,若点
 ,
, 分别在边
分别在边 ,
, 上,则
上,则 __________
__________ .(填>、<或=)
.(填>、<或=)
(2)发现证明:如图②,将图①中的
 绕点
绕点 旋转,当点
旋转,当点 在
在 外部,点
外部,点 在
在 内部时,求证:
内部时,求证: .
.
(深入研究)(3)如图③,
 和
和 都是等边三角形,点
都是等边三角形,点 ,
, ,
, 在同一条直线上,则
在同一条直线上,则 的度数为__________;线段
的度数为__________;线段 ,
, 之间的数量关系为__________.
之间的数量关系为__________.
(4)如图④,
 和
和 都是等腰直角三角形,
都是等腰直角三角形, ,点
,点 、
、 、
、 在同一直线上,
在同一直线上, 为
为 中
中 边上的高,则
边上的高,则 的度数为__________;线段
的度数为__________;线段 ,
, ,
, 之间的数量关系为__________.
之间的数量关系为__________.
(拓展提升)(5)如图⑤,
 和
和 都是等腰直角三角形,
都是等腰直角三角形, ,将
,将 绕点
绕点 逆时针旋转,连结
逆时针旋转,连结 、
、 .当
.当 ,
, 时,在旋转过程中,
时,在旋转过程中, 与
与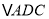 的面积和的最大值为__________.
的面积和的最大值为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,顶点B的坐标为(3,
 ),点C的坐标为(1,0),且∠B=60°,点P为斜边OB上的一个动点,则PA+PC的最小值为_____.
),点C的坐标为(1,0),且∠B=60°,点P为斜边OB上的一个动点,则PA+PC的最小值为_____.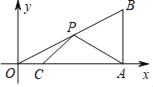
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图锐角△ABC,若∠ABC=40°,∠ACB=70°,点D、E在边AB、AC上,CD与BE交于点H.
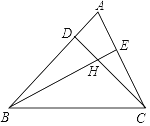
(1)若BE⊥AC,CD⊥AB,求∠BHC的度数.
(2)若BE、CD平分∠ABC和∠ACB,求∠BHC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场今年2月份的营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元.求3月份到5月份营业额的月平均增长率.
相关试题

