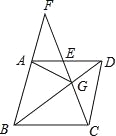
【题目】如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.
(1)求证:AG=CG.
(2)求证:AG2=GEGF.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析: (1)连接AC,根据菱形对角线互相垂直平分,G在AC的中垂线上,从而AG=CG;(2)易证△AEG∽△FGA,利用对应边成比例可得到结论.
试题解析:(1)连接AC,在菱形ABCD中,AC、BD为对角线,∴BD垂直平分AC.∵G是BD上一点,∴AG=CG.
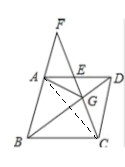
(2)∵AG=GC,∴∠GAC=∠GCA.∵AD=CD,∴∠DAC=∠DCA.∴∠DAC-∠GAC=∠DCA-∠GCA,即∠DCG=∠DAG.,∵AB∥CD,∴∠DCG=∠F,∴∠F=∠DAG.又∵∠AGF=∠AGE,∴△AEG∽△FGA,∴![]() .∴AG2=GEGF.
.∴AG2=GEGF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,BC的延长线与AD的延长线交于点E.
(1)若∠A=60°,求BC的长;
(2)若sinA=
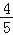 ,求AD的长.
,求AD的长.(注意:本题中的计算过程和结果均保留根号)

-
科目: 来源: 题型:
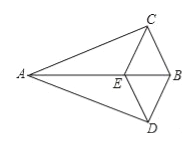
查看答案和解析>>【题目】如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.求证:
(1)∠CEB=∠CBE;
(2)四边形BCED是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种细胞的平均直径是0.00000085米,将0.00000085用科学记数法表示为( )
A. 8.5×10﹣7 B. 0.85×10﹣7 C. 8.5×10﹣6 D. 85×10﹣6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=
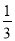 AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )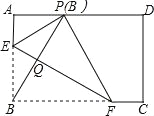
A.①② B.②③ C.①③ D.①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题“对于正整数a,关于 x 的一元二次方程ax2 -4x+1=0 没有实数根”,能说明这个命题是假命题的一个反例是a=___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是等腰三角形,AB=AC.
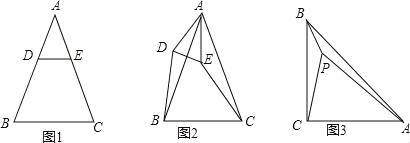
(1)特殊情形:如图1,当DE∥BC时,有DB EC.(填“>”,“<”或“=”)
(2)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.
相关试题

