【题目】如图,数轴上A、B两点分别对应有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|,利用数形结合思想回答下列问题:
![]()
(1)数轴上表示2和10两点之间的距离是 ,数轴上表示2和﹣10两点之间的距离是 ;
(2)数轴上,x和﹣2两点之间的距离是 ;
(3)若x表示一个有理数,则|x﹣1|+|x+2|有最小值吗?若有,请求出最小值,若没有,写出理由.
参考答案:
【答案】(1)8,12;(2)|x+2|;(3)3
【解析】
(1)结合数轴即可求距离;
(2)由绝对值的性质可以表示![]() 与
与![]() 之间的距离为
之间的距离为![]() ;
;
(3)当![]() 时有最小值,最小值就是1与
时有最小值,最小值就是1与![]() 之间的距离.
之间的距离.
解:(1)2与10之间的距离是8,2与![]() 之间的距离是12,
之间的距离是12,
故答案为8,12;
(2)表示![]() 与
与![]() 之间的距离为
之间的距离为![]() ,
,
故答案为![]() ;
;
(3)![]() 表示数轴上
表示数轴上![]() 与1的两点之间与
与1的两点之间与![]() 和
和![]() 的两点之间的距离和,
的两点之间的距离和,
利用数轴就可以发现:当![]() 时有最小值,最小值就是1与
时有最小值,最小值就是1与![]() 之间的距离,
之间的距离,
即![]() 的最小值为3.
的最小值为3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,∠BAD=60°,AB=2,E是DC边上一个动点,F是AB边上一点,∠AEF=30°.设DE=x,图中某条线段长为y,y与x满足的函数关系的图象大致如图所示,则这条线段可能是图中的( ).

A. 线段EC B. 线段AE C. 线段EF D. 线段BF
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是反映一辆出租车从甲地到乙地的速度(千米/时)与时间(分钟)的关系图象;根据图象,回答下列问题:
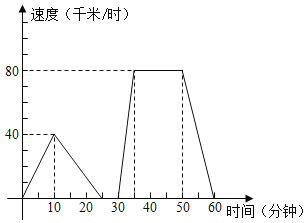
(1)汽车从出发到最后停止共经过了多长时间?它的最高时速是多少?
(2)汽车在哪段时间保持匀速行驶?时速是多少?
(3)出发后25分钟到30分钟之间可能发生了什么情况?
(4)用自己的语言大致描述这辆汽车的行驶情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某餐厅中,一张桌子可坐6人,有如图所示的两种摆放方式:

(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌.若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、CD于M、N两点.若AM=4,则BM=_____,ON=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 (
( 为常数),下列说法正确的是( ).
为常数),下列说法正确的是( ).A. 对任意实数
 ,函数与
,函数与 轴都没有交点
轴都没有交点B. 存在实数
 ,满足当
,满足当 时,函数
时,函数 的值都随
的值都随 的增大而减小
的增大而减小C.
 取不同的值时,二次函数
取不同的值时,二次函数 的顶点始终在同一条直线上
的顶点始终在同一条直线上D. 对任意实数
 ,抛物线
,抛物线 都必定经过唯一定点
都必定经过唯一定点 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(10,0)、C(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为_____.

相关试题

