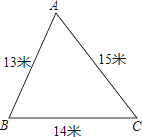
【题目】学校校内有一块如图所示的三角形空地ABC,计划将这块空地建成一个花园,以美化校园环境,预计花园每平方米造价为60元,学校修建这个花园需要投资多少元?
参考答案:
【答案】5040元
【解析】
过点D作AD⊥BC于点D,设BD=x,则CD=14-x,再根据勾股定理求出x的值,进而可得出AD的长,由三角形的面积公式即可得出结论.
过点D作AD⊥BC于点D,
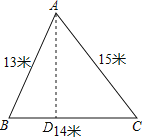
设BD=x,则CD=14-x,
在Rt△ABD与Rt△ACD中,
∵AD2=AB2-BD2,AD2=AC2-CD2,
∴AB2-BD2=AC2-CD2,即132-x2=152-(14-x)2,解得x=5,
∴AD2=AB2-BD2=132-52=144,
∴AD=12(米),
∴学校修建这个花园的费用=60×![]() ×14×12=5040(元).
×14×12=5040(元).
答:学校修建这个花园需要投资5040元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识解决下列问题.

(1)求△ABC的面积;
(2)判断△ABC是什么形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,必然事件是( )
A.抛掷1个均匀的骰子,出现6点向上
B.两直线被第三条直线所截,同位角相等
C.366人中至少有2人的生日相同
D.实数的绝对值是非负数 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,∠BAC=25°,则∠ADC=( )
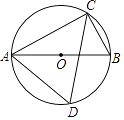
A.25
B.30°
C.45°
D.65° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,E是AD的中点,AB=8
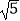 ,F是线段CE上的动点,则BF的最小值是( )
,F是线段CE上的动点,则BF的最小值是( )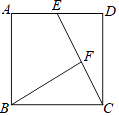
A.10
B.12
C.16
D.18 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知∠MON=60°,A、B两点同时从点O出发,点A以每秒x个单位长度沿射线ON匀速运动,点B以每秒y个单位长度沿射线OM匀速运动.

(1)若运动1s时,点A运动的路程比点B运动路程的2倍还多1个单位长度,运动3s时,点A、点B的运动路程之和为12个单位长度,则x=____,y=____;
(2)如图2,点C为△ABO三条内角平分线交点,连接BC、AC,在点A、B的运动过程中,∠ACB的度数是否发生变化?若不发生变化,求其值;若发生变化,请说明理由;
(3)如图3,在(2)的条件下,连接OC并延长,与∠ABM的角平分线交于点P,与AB交于点Q.
①试说明∠PBQ=∠ACQ;
②在△BCP中,如果有一个角是另一个角的2倍,请直接写出∠BAO的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将正方形ABCD的边AB沿AE折叠,使点B落在对角线AC上,则∠BAE的度数为 .
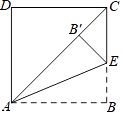
相关试题

