【题目】如图,正方形ABCD中,E是AD的中点,AB=8 ![]() ,F是线段CE上的动点,则BF的最小值是( )
,F是线段CE上的动点,则BF的最小值是( )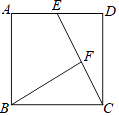
A.10
B.12
C.16
D.18
参考答案:
【答案】C
【解析】解:当BF⊥EC时,BF有最小值,如图,
则∠BFC=90°,
∵E是AD的中点,
∴ED= ![]() AD=
AD= ![]() ×
× ![]() =4
=4 ![]() ,
,
∵四边形ABCD是正方形,
∴∠D=90°,BC=CD=AB=8 ![]() ,
,
Rt△EDC中,由勾股定理得:EC= ![]() =20,
=20,
∵∠BFC=∠D=90°,∠FBC=∠ECD,
∴△BFC∽△CDE,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴BF=16,
所以答案是:C.
【考点精析】通过灵活运用正方形的性质和相似三角形的判定与性质,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,必然事件是( )
A.抛掷1个均匀的骰子,出现6点向上
B.两直线被第三条直线所截,同位角相等
C.366人中至少有2人的生日相同
D.实数的绝对值是非负数 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,∠BAC=25°,则∠ADC=( )
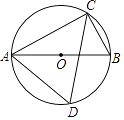
A.25
B.30°
C.45°
D.65° -
科目: 来源: 题型:
查看答案和解析>>【题目】学校校内有一块如图所示的三角形空地ABC,计划将这块空地建成一个花园,以美化校园环境,预计花园每平方米造价为60元,学校修建这个花园需要投资多少元?
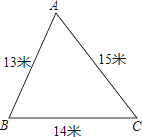
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知∠MON=60°,A、B两点同时从点O出发,点A以每秒x个单位长度沿射线ON匀速运动,点B以每秒y个单位长度沿射线OM匀速运动.

(1)若运动1s时,点A运动的路程比点B运动路程的2倍还多1个单位长度,运动3s时,点A、点B的运动路程之和为12个单位长度,则x=____,y=____;
(2)如图2,点C为△ABO三条内角平分线交点,连接BC、AC,在点A、B的运动过程中,∠ACB的度数是否发生变化?若不发生变化,求其值;若发生变化,请说明理由;
(3)如图3,在(2)的条件下,连接OC并延长,与∠ABM的角平分线交于点P,与AB交于点Q.
①试说明∠PBQ=∠ACQ;
②在△BCP中,如果有一个角是另一个角的2倍,请直接写出∠BAO的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将正方形ABCD的边AB沿AE折叠,使点B落在对角线AC上,则∠BAE的度数为 .
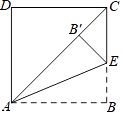
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(a,0),点B(2﹣a,0),且A在B的左边,点C(1,﹣1),连接AC,BC,若在AB,BC,AC所围成区域内(含边界),横坐标和纵坐标都为整数的点的个数为4个,那么a的取值范围为( )
A. ﹣1<a≤0B. 0≤a<1C. ﹣1<a<1D. ﹣2<a<2
相关试题

