【题目】对数(生于公元250年左右)是中国数字史上伟大的数学家,在世界数学史上,也占着重要的地位,他的杰作《九章算术法》和《海岛算经》是我国宝贵的数学遗产.
(1)其中一卷书研究的对象全是有关高与距离的测量,所使用的工具也都是利用垂直关系所连接起来的测杆与横棒,所有问题都是利用两次或多次测量所得的数据,来推算可望而不可及的目标的高、深、广、远,此书收集于明成祖时编修的永乐大典中,现保存在英国剑桥大学图书馆,该卷书是 海岛算经 ;
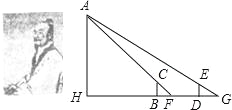
(2)在(1)中提到刘嶶的杰作中,记载的第一个问题的大意是:在如图所示的示意图中,要测量海岛上一座山峰的高度AH,立两根高3丈的标杆BC和DE,两杆之间的距离BD=1000步,点D、B、H成一线,从B处退行123步到点F处,人的眼睛贴着地面观察点A,点A、C、F也成一线,从D处退行127步到点G处,人的眼睛贴着地面观察点A,点A,E,G也成一线,求AH有多少丈,HB有多少步(这里1步=6尺,1丈=10尺)
参考答案:
【答案】(1)《海岛算经》;(2)AH为753丈,HB为30750步.
【解析】
试题分析:(1)根据历史常识可得到答案;
(2)根据题意得出△FCB∽△FAH,△EDG∽△AHG,进而利用相似三角形的性质求出即可.
试题解析:(1)《海岛算经》;
(2)由题意,得,AH⊥HG,CB⊥HG,∴∠AHF=90°,∠CBF=90°,∴∠AHF=∠CBF,
∵∠AFB=∠CFB,∴△CBF∽△AHF,∴![]() ,同理可得
,同理可得![]() ,
,
∵BF=123,BD=1000,DG=127,
∴HF=HB+123,HG=HB+1000+127=HB+1127,
∴![]() =
=![]() ,
,![]() =
=![]() ,
,
解得HB=30750,HA=753,
答:AH为753丈,HB为30750步.
-
科目: 来源: 题型:
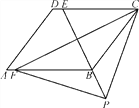
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC,其中正确结论的个数为( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A.位似图形可以通过平移而相互得到
B.位似图形的对应边平行且相等
C.位似图形的位似中心不只有一个
D.位似中心到对应点的距离之比都相等 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
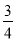 x2﹣
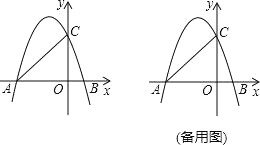
x2﹣ x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC,BC,把△ABC沿x轴向右平移得到△A′B′C′,AB边上的点O平移到点O′.
x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC,BC,把△ABC沿x轴向右平移得到△A′B′C′,AB边上的点O平移到点O′.(1)求点B、C的坐标及抛物线的对称轴;
(2)在平移的过程中,设点B关于直线A′C′的对称点为点F,当点F落在直线AC上时,求△ABC平移的距离;
(3)在平移过程中,连接CA′,CO′,求△A′CO′周长的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AE⊥BC,垂足为点E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,∠1=∠2.

(1)若CF=2,AE=3,求BE的长;
(2)求证:∠CEG=
 ∠AGE.
∠AGE. -
科目: 来源: 题型:
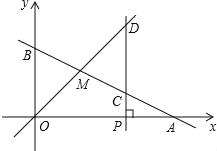
查看答案和解析>>【题目】如图,已知函数y=kx+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点A的坐标为(6,0),点M的横坐标为2,过点P(a,0),作x轴的垂线,分别交函数y=kx+b和y=x的图象于点C、D.
(1)求函数y=kx+b的表达式;
(2)若点M是线段OD的中点,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面关于平行四边形的说法中错误的是( )
A. 平行四边形的两条对角线相等
B. 平行四边形的两条对角线互相平分
C. 平行四边形的对角相等
D. 平行四边形的对边相等
相关试题

