【题目】数学课上,我们知道可以用图形的面积来解释一些代数恒等式,如图1可以解释完全平方公式(a+b)2=a2+2ab+b2 . 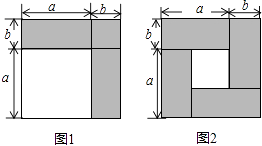
(1)如图2,请用不同的代数式表示图中阴影部分的面积,由此,你能得到怎样的等式?
(2)请说明这个等式成立;
(3)已知(2m+n)2=13,(2m﹣n)2=5,请利用上述等式求mn.
参考答案:
【答案】
(1)解:阴影部分的面积为:4ab或(a+b)2﹣(a﹣b)2,
得到等式:4ab=(a+b)2﹣(a﹣b)2
(2)解:右边=a2+2ab+b2﹣(a2﹣2ab+b2)=a2+2ab+b2﹣a2+2ab﹣b2=4ab=左边,即等式成立
(3)解:(2m+n)2﹣(2m﹣n)2=4×2mn,
13﹣5=8mn,
mn=1
【解析】(1)根据阴影部分的面积=4个小长方形的面积=大正方形的面积﹣小正方形的面积,利用完全平方公式,即可解答;(2)根据完全平方公式解答;(3)根据平方差公式解答.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中,不能判定四边形为平行四边形的是( )
A.一组对边平行,另一组对边相等
B.一组对边平行且相等
C.两组对边分别平行
D.对角线互相平分 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a+2a=3a2B.a3a2=a5C.(a4)2=a6D.a4+a2=a4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b<0;②abc>0;③4a﹣2b+c>0;④a+c>0,其中正确结论的个数为( ).

A.4个 B.3个 C.2个 D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一次函数y=﹣2x+b(b为常数)的图象经过第二、三、四象限,则b的值可以是(写出一个即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角△ABC中,∠ACB=90°,O是AB边上的中点,点D,E分别在AC,BC边上,且∠DOE=90°,DE交OC于P,下列结论正确的共有( )
①图中的全等三角形共有3对;②AD=CE;③∠CDO=∠BEO;④OC=DC+CE;⑤△ABC的面积是四边形DOEC面积的2倍。
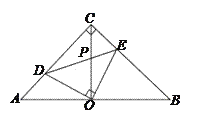
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知4x=3y,求代数式(x﹣2y)2﹣(x﹣y)(x+y)﹣2y2的值.
相关试题

