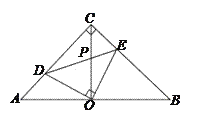
【题目】如图,在等腰直角△ABC中,∠ACB=90°,O是AB边上的中点,点D,E分别在AC,BC边上,且∠DOE=90°,DE交OC于P,下列结论正确的共有( )
①图中的全等三角形共有3对;②AD=CE;③∠CDO=∠BEO;④OC=DC+CE;⑤△ABC的面积是四边形DOEC面积的2倍。
A. 2个 B. 3个 C. 4个 D. 5个
参考答案:
【答案】C
【解析】∵在等腰直角△ABC中,∠ACB=90°,O是AB边上的中点,
∴∠A=∠B=45°,CO=AO=BO,CO⊥AB,∠ACO=∠BCO=45°,
∴∠A=∠ECO,∠B=∠DCO,∠COA=∠COB=90°,
∵∠DOE=90°,
∴∠AOD=∠COE=90°∠COD,∠COD=∠BOE=90∠COE,
在△COE和△AOD中
∠ECO=∠ACO=AO∠COE=∠DOA
∴△COE≌△AOD(ASA),
同理△COD≌△BOE,
∴S△COE=S△AOD,AD=CE,∠CDO=∠BEO,△ABC的面积是四边形DOEC面积的2倍,
在△AOC和△BOC中
CO=COAC=BCAO=BO
∴△AOC≌△BOC,
∵AD=CE,
∴CD+CE=AC,
∵∠COA=90,
∴CO<AC,
∴OC=DC+CE错误;
即①②③⑤正确,④错误;
故答案为:C
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b<0;②abc>0;③4a﹣2b+c>0;④a+c>0,其中正确结论的个数为( ).

A.4个 B.3个 C.2个 D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,我们知道可以用图形的面积来解释一些代数恒等式,如图1可以解释完全平方公式(a+b)2=a2+2ab+b2 .
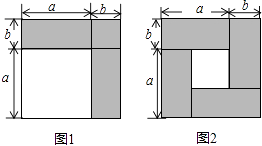
(1)如图2,请用不同的代数式表示图中阴影部分的面积,由此,你能得到怎样的等式?
(2)请说明这个等式成立;
(3)已知(2m+n)2=13,(2m﹣n)2=5,请利用上述等式求mn. -
科目: 来源: 题型:
查看答案和解析>>【题目】若一次函数y=﹣2x+b(b为常数)的图象经过第二、三、四象限,则b的值可以是(写出一个即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知4x=3y,求代数式(x﹣2y)2﹣(x﹣y)(x+y)﹣2y2的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将△ABC中纸片沿DE折叠,使点A落在四边形DBCE内点A′的位置,探索∠A与∠1+∠2之间的数量关系,并说明理由
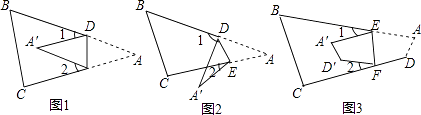
(1)如图2,将△ABC中纸片沿DE折叠,使点A落在四边形DBCE的外部点A′的位置,探索∠A与∠1、∠2之间的数量关系,并说明理由;
(2)如图3,将四边形ABCD沿EF折叠,使点A、D落在四边形BCFE内部点A′D′的位置,请直接写出∠A、∠D、∠1与∠2之间的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC为等边三角形,点D为直线BC上一动点(点D不与点B,点C重合)。以AD为边作等边三角形ADE,连接CE。

(1)如图(1),当点D在边BC上时。
①求证:△ABD≌△ACE;
②直接判断结论BC=DC+CE是否成立(不需证明);
(2)如图2,当点D在边BC的延长线上时,其他条件不变,请写出BC,DC,CE之间存在的数量关系,并写出证明过程。
相关试题

