【题目】一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,设先发出车辆行驶的时间为 xh , 两车之间的距离为ykm,图中的折线表示 y与x之间的函数关系。根据图象回答下列问题:
(1)慢车的速度为________ km/h,快车的速度为__________km/h;
(2)求线段CD所表示的y与x之间的函数关系式,并写出自变量 x的取值范围;
(3)当 x取何值时,两车之间的距离为300 km?

参考答案:
【答案】(1)80,120;(2) ![]() ;(3)1.2或4.2.
;(3)1.2或4.2.
【解析】整体分析:
(1)先利用前0.5小时的路程除以时间求出一辆车的速度,再利用相遇问题根据2.7小时列式求解即可得到另一辆车的速度;(2)理解点C和点D的意义,并求出它们的坐标,再求CD所在直线的函数关系式;(3)注意分类,两车相遇前相距300km或两车相遇后相距300km.
解:(1)(480-440)÷0.5=80km/h,
440÷(2.7-0.5)-80=120km/h,
所以慢车速度为80km/h,快车速度为120km/h;
故答案为80,120;
(2)因为快车走完全程所需时间为480÷120=4(h),
所以点D的横坐标为4.5,
纵坐标为(120+80)×(4.5-2.7)=360,
即点D(4.5,360);
又点C(2.7,0).
设直线CD的解析式为y=kx+b,则
![]() ,解得
,解得![]() .
.
则y=200x-540,且2.7≤x≤4.5
所以线段CD所表示的y与x之间的函数关系式为y=200x-540,,自变量x的取值范围是2.7≤x≤4.5.
(3)由题意,可知两车行驶的过程中有2次两车之间的距离为300km.
即(80+120)×(x-0.5)=440-300,解得x=1.2h;
或(80+120)×(x-2.7)=300,解得x=4.2h.
故x=1.2h或4.2h,两车之间的距离为300km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于两个两位数m和n,将其中任意一个两位数的十位上的数字和个位上的数字分别放置于另一个两位数十位上数字与个位上的数字之间和个位上的数字的右边,就可以得到两个新四位数,把这两个新四位数的和与11的商记为F(m,n)。例如:当m=36,n=10时,将m十位上的3放置n中1与0之间,将m个位上的6位置于n中0的右边,得到1306.将n个十位上的1放置于m中3和6之间,将n个位上的0放置于m中6的右边,得到3160。这两个新四位数的和为1306+3160=4466,4466÷11=406,所以F(36,10)=406。
(1)计算:F(20,18);
(2)若a=10+x,b=10y+8(0≤x≤9,1≤y≤9,x,y都是自然数)。当150 F(a,36)+ F(b,49)=62767时,求F(5a,b)的最大值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知ab<0,
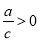 ,且|c|>|b|>|a|,数轴上a、b、c对应的点是A、B、C.
,且|c|>|b|>|a|,数轴上a、b、c对应的点是A、B、C.(1) 若|a|=-a时,请在数轴上标出A、B、C的大致位置;
(2) 在(1)的条件下,化简:|a-b|-|b+c|+|c+a|.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如表:方程1、方程2、方程3…是按照一定规律排列的一列方程:
序号
方程
方程的解
1
 ﹣
﹣ =1
=1x1=3,x2=4
2
 ﹣
﹣ =1
=1x1=4,x2=6
3
 ﹣
﹣ =1
=1x1=5,x2=8
…
…
…
(1)若方程
 ﹣
﹣ =1(a>b)的解是x1=6,x2=10,则a=_____b=_____.
=1(a>b)的解是x1=6,x2=10,则a=_____b=_____.(2)请写出这列方程中第n个方程:_____ 方程的解:_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
, ,
, ,
, ,
, 平分
平分

(1)说明:
 ;(2)求
;(2)求 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=kx+3(k<0)分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,过点P作x轴的垂线交直线AB于点C,设运动时间为t秒.
(1)当k=-1时,线段OA上另有一动点Q由点A向点O运动,它与点P以相同速度同时出发,当点P到达点A时两点同时停止运动(如图1).
①直接写出t=1秒时C、Q两点的坐标;
②若以Q、C、A为顶点的三角形与△AOB相似,求t的值.
(2)当k=
 时,设以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D(如图2),
时,设以C为顶点的抛物线y=(x+m)2+n与直线AB的另一交点为D(如图2),①求CD的长;
②设△COD的OC边上的高为h,当t为何值时,h的值最大?


-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂有新、旧两台机器,上半年,新机器平均每天比旧机器多生产50件产品,新机器生产600件产品所用的时间与旧机器生产450件产品所用的时间相同.
(1)求上半年新、旧机器日均产品数;
(2)下半年,新机器提高了生产效率,而旧机器由于不断损耗,生产效率降低,经测算,新机器日均产品数提高的百分数是旧机器日均产品数降低的百分数的2倍,结果新机器生产960件产品所用的时间与旧机器生产540件产品所用的时间相同,求新机器日均产品比旧机器多多少件?
相关试题

