【题目】如图,在直角坐标系中,OC OD,OC OD ,DC 的延长线交 y 轴正半轴上点 B ,过点C 作CA BD 交 x 轴负半轴于点A .
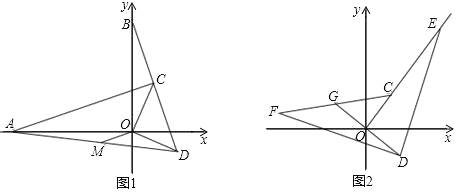
(1)如图1,求证:OAOB
(2)如图1,连AD,作OM ∥AC交AD于点M,求证: BC 2OM
(3)如图2,点E为OC 的延长线上一点,连DE,过点D作DFDE且DF DE ,连CF 交 DO 的延长线于点G 若OG 4,求CE 的长.
参考答案:
【答案】(1)见解析;(2)见解析;(3)CE=OT=8.
【解析】
(1)由OC⊥OD,CA⊥BD知∠COD=∠BCA=∠AOB=90°,从而得∠AOC=∠BOD,∠OBD=∠OAC,结合OC=OD证△AOC≌△BOD可得答案;
(2)作AN∥OD,交OM延长线于点N,先证△BOC≌△OAN得BC=ON,AN=OC=OD,再证△AMN≌△DMO得OM=MN=![]() ON,从而得证;
ON,从而得证;
(3)作FT⊥DG,交DG延长线于点T,先证△FTD≌△DOE得FT=OD=OC,DT=OE,再证△FTG≌△COG得OT=2OG=8,根据OE=DT,OC=OD可得CE=OT.
解:(1)∵OC⊥OD,CA⊥BD,
∴∠COD=∠BCA=∠AOB=90°,
∴∠BOC+∠COE=90°, ∠DOE+∠COE=90°,
∴∠BOC=∠DOE,
∴∠AOC=∠BOD,
同理可证∠OBD=∠OAC,
在△AOC和△BOD中,
∵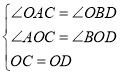 ,
,
∴△AOC≌△BOD(AAS),
∴OA=OB;
(2)如图1,过点A作AN∥OD,交OM延长线于点N,
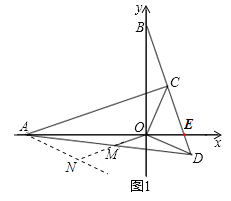
则∠OAN+∠AOD=180°,
∵∠AOB=∠COD=90°,
∴∠AOD+∠BOC=180°,
∴∠OAN=∠BOC,
又∵OM∥AC,
∴∠AON=∠CAO,
由(1)知∠CAO=∠OBC,
∴∠AON=∠OBC,
又∵OA=OB,
∴△BOC≌△OAN(ASA),
∴BC=ON,AN=OC=OD,
∵AN∥OD,
∴∠MAN=∠MDO,∠MNA=∠MOD,
∴△AMN≌△DMO(ASA),
∴OM=MN=![]() ON,即ON=2OM,
ON,即ON=2OM,
∴BC=2OM;
(3)如图2,过点F作FT⊥DG,交DG延长线于点T,
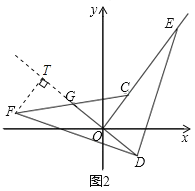
则∠FTD=∠DOE=90°,
∴∠ODE+∠OED=90°,
又∵DE⊥DF,
∴∠ODE+∠FDT=90°,
∴∠OED=∠TDF,
∵DE=DF,
∴△FTD≌△DOE(AAS),
∴FT=OD,DT=OE,
∵OD=OC,
∴FT=OC,
∵∠FTG=∠COG=90°,∠FGT=∠CGO,
∴△FTG≌△COG(AAS),
∴OT=2OG=8,
∵OE=DT,OC=OD,
∴CE=OT=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程组
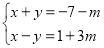 的解满足
的解满足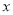 为非正数,
为非正数,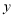 为负数.
为负数.(1)求
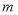 的取值范围
的取值范围(2)在(1)的条件下,若不等式
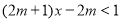 的解为
的解为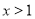 ,求整数
,求整数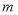 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1,此时AP1=
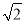 ;将位置①的三角形绕点P1顺时针旋转到位置②可得到点P2,此时AP2=
;将位置①的三角形绕点P1顺时针旋转到位置②可得到点P2,此时AP2=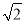 +1;将位置②的三角形绕点P2顺时针旋转到位置③可得到点P3时,AP3=
+1;将位置②的三角形绕点P2顺时针旋转到位置③可得到点P3时,AP3=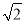 +2…按此规律继续旋转,直至得到点P2026为止,则AP2016= .
+2…按此规律继续旋转,直至得到点P2026为止,则AP2016= .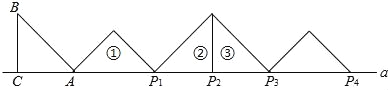
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(2,0),B ( 2,0),C为 y 轴负半轴上一点,D是第四象限内一动点,且始终有BDA 2ACO 成立,过C 点作CE BD 于点 E .
(1)求证:DAC DBC ;
(2)若点 F 在 AD 的延长线上,求证:CD 平分BDF ;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=24厘米,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______厘米/秒时,能够在某一时刻使△BPD与△CQP全等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度
 (厘米)与燃烧时间
(厘米)与燃烧时间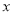 (小时)之间的关系如图所示,其中乙蜡烛燃烧时
(小时)之间的关系如图所示,其中乙蜡烛燃烧时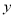 与
与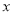 之间的函数关系式是
之间的函数关系式是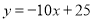 .
. 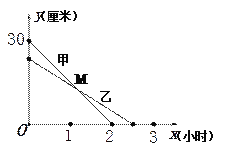
(1)甲蜡烛燃烧前的高度是_________厘米,乙蜡烛燃烧的时间是________小时.
(2)求甲蜡烛燃烧时
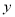 与
与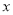 之间的函数关系式.
之间的函数关系式. (3)求出图中交点
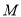 的坐标,并说明点
的坐标,并说明点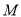 的实际意义.
的实际意义. -
科目: 来源: 题型:
查看答案和解析>>【题目】小赵为班级购买笔记本作为晚会上的奖品,回来时向生活委员交账说“一共买了36本,有两种规格,单价分别为1.8元和2.6元,去时我领了100元,现在找回27.6元.”生活委员算了一下,认为小赵稿错了.
(1)请你用方程的知识说明小赵为什么搞错了.
(2)小赵一想,发觉的确不对,因为他把自己口袋里的零用钱一起当做找回的钱给了生活委员,如果设购买单价为1.8元的笔记本
 本,并且小赵的零用钱数目是整数,且少于3元,试求出小赵零用钱的数目.
本,并且小赵的零用钱数目是整数,且少于3元,试求出小赵零用钱的数目.
相关试题

