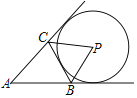
【题目】如图,△ABC中,BC=4,⊙P与△ABC的边或边的延长线相切.若⊙P半径为2,△ABC的面积为5,则△ABC的周长为( )
A.8B.10C.13D.14
参考答案:
【答案】C
【解析】
根据三角形的面积公式以及切线长定理即可求出答案.
连接PE、PF、PG,AP,
由题意可知:∠PEC=∠PFA=PGA=90°,
∴S△PBC=![]() BCPE=
BCPE=![]() ×4×2=4,
×4×2=4,
∴由切线长定理可知:S△PFC+S△PBG=S△PBC=4,
∴S四边形AFPG=S△ABC+S△PFC+S△PBG+S△PBC=5+4+4=13,
∴由切线长定理可知:S△APG=![]() S四边形AFPG=
S四边形AFPG=![]() ,
,
∴![]() =
=![]() ×AGPG,
×AGPG,
∴AG=![]() ,
,
由切线长定理可知:CE=CF,BE=BG,
∴△ABC的周长为AC+AB+CE+BE
=AC+AB+CF+BG
=AF+AG
=2AG
=13,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】佳佳调査了七年级400名学生到校的方式,根据调查结果绘制出统计图的一部分如图:
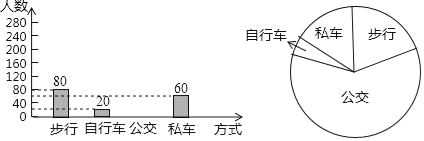
(1)补全条形统计图;
(2)求扇形统计图中表示“步行”的扇形圆心角的度数;
(3)估计在3000名学生中乘公交的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图分别是某款篮球架的实物图与示意图,已知
 于点
于点 ,底座
,底座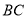 的长为
的长为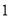 米,底座
米,底座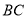 与支架
与支架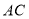 所成的角
所成的角 ,点
,点 在支架
在支架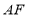 上,篮板底部支架
上,篮板底部支架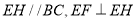 于点
于点 ,已知
,已知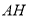 长
长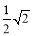 米,
米, 长
长 米,
米,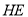 长
长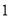 米.
米.(1)求篮板底部支架
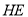 与
与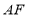 支架所成的角
支架所成的角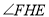 的度数.
的度数.(2)求篮板底部点
 到地面的距离.(结果保留根号)
到地面的距离.(结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图1,在△ABC中,∠ACB=90°,BC=AC,点D在AB上,DE⊥AB交BC于E,点F是AE的中点
(1)写出线段FD与线段FC的关系并证明;
(2)如图2,将△BDE绕点B逆时针旋转α(0°<α<90°),其它条件不变,线段FD与线段FC的关系是否变化,写出你的结论并证明;
(3)将△BDE绕点B逆时针旋转一周,如果BC=4,BE=2
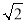 ,直接写出线段BF的范围.
,直接写出线段BF的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式:
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
7
25
0.01
B
m
n
0.01
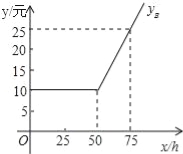
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m= ;n=
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知
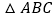 是等腰直角三角形,
是等腰直角三角形, ,点D是BC的中点
,点D是BC的中点 作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.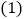 试猜想线段BG和AE的数量关系是______;
试猜想线段BG和AE的数量关系是______;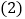 将正方形DEFG绕点D逆时针方向旋转
将正方形DEFG绕点D逆时针方向旋转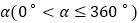 ,
, 判断
判断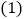 中的结论是否仍然成立?请利用图2证明你的结论;
中的结论是否仍然成立?请利用图2证明你的结论; 若
若 ,当AE取最大值时,求AF的值.
,当AE取最大值时,求AF的值.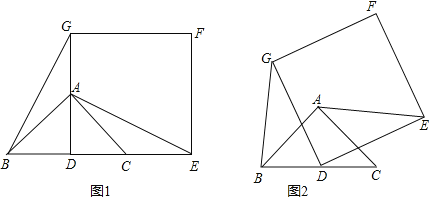
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线
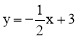 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数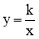 的图象经过点M,N.
的图象经过点M,N.
(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
相关试题

