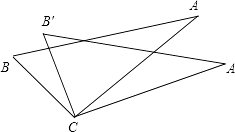
【题目】如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( ) 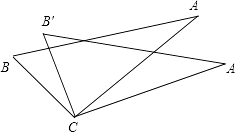
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】B
【解析】解:当①②③为条件,④为结论时:
∵∠A′CA=∠B′CB,
∴∠A′CB′=∠ACB,
∵BC=B′C,AC=A′C,
∴△A′CB′≌△ACB,
∴AB=A′B′,
当①②④为条件,③为结论时:
∵BC=B′C,AC=A′C,AB=A′B′
∴△A′CB′≌△ACB,
∴∠A′CB′=∠ACB,
∴∠A′CA=∠B′CB.
故选B.
根据全等三角形的判定定理,可以推出①②③为条件,④为结论,依据是“SAS”;①②④为条件,③为结论,依据是“SSS”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=90°,∠EBE′=90°,AB=BC,BE=BE′,若AE=1,BE=2,∠BE′C=135°,求EC的长.

-
科目: 来源: 题型:
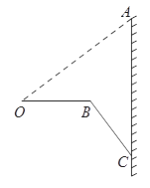
查看答案和解析>>【题目】如图,高铁列车座位后面的小桌板收起时可以近似地看作与地面垂直,展开小桌板后,桌面会保持水平.如图的实线是小桌板展开后的示意图,其中OB表示小桌面的宽度,BC表示小桌板的支架.连接OA,此时OA=75厘米,∠AOB=∠ACB=37°,且支架长BC与桌面宽OB的长度之和等于OA的长度,求点B到AC的距离.(参考数据:
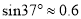 ,
, 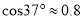 ,
, 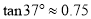 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件是必然事件的是( )
A.明天太阳从西方升起
B.打开电视机,正在播放广告
C.掷一枚硬币,正面朝上
D.任意一个三角形,它的内角和等于180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线
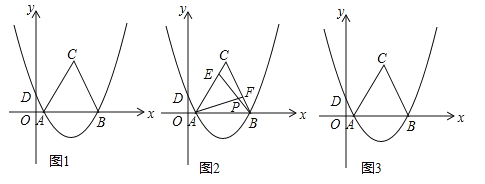
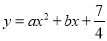 ,经过A(1,0)、B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边△ABC.
,经过A(1,0)、B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边△ABC.(1)求抛物线的解析式;
(2)在x轴上方的抛物线上是否存在点M,是S△ABM=
 S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;
S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;(3)如图2,E是线段AC上的动点,F是线段BC上的动点,AF与BE相交于点P.
①若CE=BF,试猜想AF与BE的数量关系及∠APB的度数,并说明理由;
②若AF=BE,当点E由A运动到C时,请直接写出点P经过的路径长(不需要写过程).
相关试题

