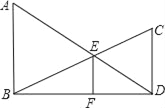
【题目】已知:如图,AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC相交于点E,EF⊥BD,垂足为F,我们可以证明![]() 成立(不要求考生证明).
成立(不要求考生证明).
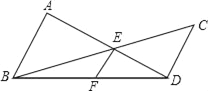
若将图中的垂线改为斜交,如图,AB∥CD,AD,BC相交于点E,过点E作EF∥AB交BD于点F,则:
(1)![]() 还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
(2)请找出S△ABD,S△BED和S△BDC间的关系式,并给出证明.
参考答案:
【答案】(1)成立(2)![]()
【解析】试题分析: (1)∵ AB∥EF,所以![]() ,∵CD∥EF,∴
,∵CD∥EF,∴![]() ,
,
∴![]() =1,∴
=1,∴![]() ,
,
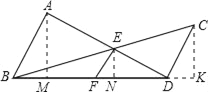
(2)分别过A作AM⊥BD于M,过E作EN⊥BD于N,过C作CK⊥BD交BD的延长线于K,由题设可得: ![]() ,∴
,∴![]() ,又∵
,又∵![]() BDAM=S△ABD,
BDAM=S△ABD, ![]() =S△BCD
=S△BCD
∴![]() BDEN=S△BED,∴
BDEN=S△BED,∴![]() .
.
试题解析:(1)成立.
证明:∵ AB∥EF,
所以![]() ,
,
∵CD∥EF,
∴![]() ,
,
∴![]() =1,
=1,
∴![]() ,
,
(2)关系式为: ![]() ,
,
证明如下:分别过A作AM⊥BD于M,过E作EN⊥BD于N,过C作CK⊥BD交BD的延长线于K,
由题设可得: ![]() ,
,
∴![]() ,
,
又∵![]() BDAM=S△ABD,
BDAM=S△ABD, ![]() =S△BCD
=S△BCD
∴![]() BDEN=S△BED,
BDEN=S△BED,
∴![]() .
.
-
科目: 来源: 题型:
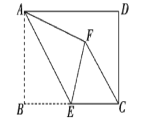
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长度为_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )

A. 4:2:1 B. 5:3:1 C. 25:12:5 D. 51:24:10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知CO1是△ABC的中线,过点O1作O1E1∥AC交BC于点E1,连接AE1交CO1于点O2;过点O2作O2E2∥AC交BC于点E2,连接AE2交CO1于点O3;过点O3作O3E3∥AC交BC于点E3,…,如此继续,可以依次得到点O4,O5,…,On和点E4,E5,…,En.则OnEn= AC.(用含n的代数式表示)
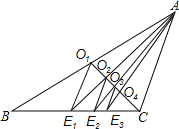
-
科目: 来源: 题型:
查看答案和解析>>【题目】列出下列问题中的函数关系式,并判断它们是否为反比例函数.
(1)某农场的粮食总产量为1 500t,则该农场人数y(人)与平均每人占有粮食量x(t)的函数关系式;
(2)在加油站,加油机显示器上显示的某一种油的单价为每升4.75元,总价从0元开始随着加油量的变化而变化,则总价y(元)与加油量x(L)的函数关系式;
(3)小明完成100m赛跑时,时间t(s)与他跑步的平均速度v(m/s)之间的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,求AP的长.
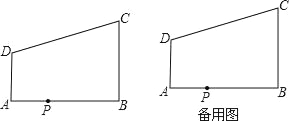
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=
 ,且使y=k成立的x值恰好有2个,则k的取值范是_____.
,且使y=k成立的x值恰好有2个,则k的取值范是_____.
相关试题

