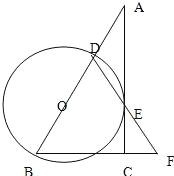
【题目】在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连接DE并延长,与BC的延长线交于点F.
(1)求证:BD=BF;
(2)若BC=6,AD=4,求⊙O的面积.
参考答案:
【答案】(1)证明详见解析;(2)16π.
【解析】
试题分析:(1)作辅助线,连接OE,根据切线的性质知OE⊥AC,已知∠ACB=90°,可知OE∥BC,得∠OED=∠F,再根据OD=OE,可知∠ODE=∠OED,从而可得∠ODE=∠F,BD=BF;
(2)根据△AOE∽△ABC,可将⊙O的半径求出,代入圆的面积公式![]() ,计算即可.
,计算即可.
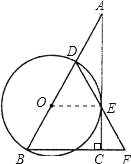
试题解析:(1)证明:如图,连接OE,
∵AC切⊙O于E,
∴OE⊥AC,
又∠ACB=90°,即BC⊥AC,
∴OE∥BC,
∴∠OED=∠F,
又OD=OE,
∴∠ODE=∠OED,
∴∠ODE=∠F,
∴BD=BF;
(2)解:设⊙O半径为r,
由OE∥BC得△AOE∽△ABC,
∴![]() ,即
,即![]() ,
,
∴![]() ﹣r﹣12=0,
﹣r﹣12=0,
解之得![]() =4,
=4,![]() =﹣3(舍),
=﹣3(舍),
经检验,r=4是原分式的解.
∴![]() 16π.
16π.
-
科目: 来源: 题型:
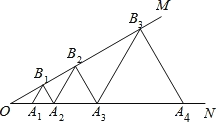
查看答案和解析>>【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△AnBnAn+1的边长为__________.
-
科目: 来源: 题型:
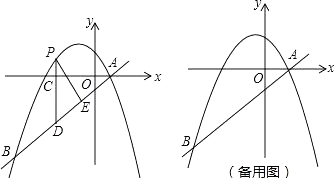
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=
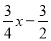 与抛物线y=
与抛物线y=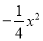 +bx+c交于A、B两点,点A在x轴上,点B的横坐标为﹣8.
+bx+c交于A、B两点,点A在x轴上,点B的横坐标为﹣8.(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值;
②连接PA,以PA为边作图示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,直接写出对应的点P的坐标.
-
科目: 来源: 题型:
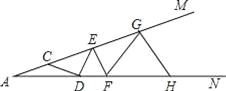
查看答案和解析>>【题目】如图,∠MAN是一钢架,且∠MAN=15°,为使钢架更加坚固,需在其内部加一些钢管CD、DE、EF…添加的钢管长度都与AC相等,则最多能添加这样的钢管______根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】新型冠状病毒平均直径为100纳米,即0.00001厘米.0.00001用科学记数法表示为( )
A.1×105B.10×10﹣6C.1×10﹣5D.0.1×10﹣4
-
科目: 来源: 题型:
查看答案和解析>>【题目】台北捷连木栅线票价及行驶时间表,如表,请问:
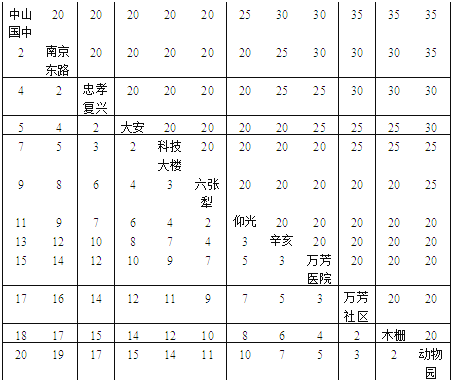
范例:忠孝复兴站至辛亥站之票价为25元,自科技大楼站至木栅站需时12分钟.
(1)某同学自南京东路站搭木栅线捷运电联车,欲至万芳社区站,投一枚50元硬币购买车票,应该找回几元?
(2)该同学于上午七时十分搭上电联车,应该何时到达万芳社区站? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=
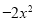 +4x+6.
+4x+6.(1)求出该函数图象的顶点坐标,对称轴,图象与x轴、y轴的交点坐标,并在下面的网格中画出这个函数的大致图象;
(2)利用函数图象回答:
①当x在什么范围内时,y随x的增大而增大?当x在什么范围内时,y随x的增大而减小?
②当x在什么范围内时,y>0?
相关试题

