【题目】解方程
(1)![]()
(2)![]()
参考答案:
【答案】(1)x=![]() (2)无解
(2)无解
【解析】
(1)首先方程两边同乘以2(x+3)去分母,然后再解一元一次方程可得x的值,再检验即可;
(2)首先方程两边同乘以3(x-2)去分母,然后再解一元一次方程可得x的值,再检验即可.
(1)![]() ,
,
去分母得:4x+2(x+3)=7,
去括号得:4x+2x+6=7,
移项得:4x+2x=7﹣6,
合并同类项得:6x=1,
把系数化为1得:x=![]() ,
,
检验:把x=![]() 代入2(x+3)≠0,
代入2(x+3)≠0,
∴分式方程的解为x=![]() ;
;
(2)![]() ,
,
去分母得:3(5x﹣4)=4x+10﹣3(x﹣2),
去括号得:15x﹣12=4x+10﹣3x+6,
移项得:15x﹣4x+3x=10+6+12,
合并同类项得:14x=28,
系数化为1得:x=2,
检验:把x=2代入3(x﹣2)=0,
∴分式方程无解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=﹣
 x+3与坐标轴分别交于点A,B,点P在抛物线y=﹣
x+3与坐标轴分别交于点A,B,点P在抛物线y=﹣  (x﹣
(x﹣  )2+4上,能使△ABP为等腰三角形的点P的个数有( )
)2+4上,能使△ABP为等腰三角形的点P的个数有( )
A.3个
B.4个
C.5个
D.6个 -
科目: 来源: 题型:
查看答案和解析>>【题目】用边长为12cm的正方形硬纸板做三棱柱盒子,每个盒子的侧面为长方形,底面为等边三角形.
(1)每个盒子需 个长方形, 个等边三角形;
(2)硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面.

现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
① 用x的代数式分别表示裁剪出的侧面和底面的个数;
② 若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD中,∠ABC的角平分线BE将边AD分成长度为5cm和6cm的两部分,则平行四边形ABCD的周长为__________________cm.
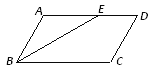
-
科目: 来源: 题型:
查看答案和解析>>【题目】两块大小一样斜边为4且含有30°角的三角板如图水平放置.将△CDE绕C点按逆时针方向旋转,当E点恰好落在AB上时,△CDE旋转了度,线段CE旋转过程中扫过的面积为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公园的门票价格如下表:
购票人数
1-50人
51-100人
100人以上
每人门票数
13元
11元
9元
实验学校初二(1)、二(2)两个班的学生共104人去公园游玩,其中二(1)班的人数不到50人,二(2)班的人数有50多人,经估算,如果两个班都以班为单位分别购票,则一共应付1240元,如果两班联合起来,作为一个团体购票,则可节省不少钱,你能否求出两个班共有多少名学生联合起来购票能省多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列一段文字,然后回答问题.
已知在平面内两点P1(x1,y1)、P2(x2,y2),其两点间的距离P1P2=
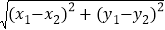 ,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.(1)已知A(2,4)、B(-3,-8),试求A、B两点间的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为4,点B的纵坐标为-1,试求A、B两点间的距离;
(3)已知一个三角形各顶点坐标为D(1,6)、E(-2,2)、F(4,2),你能判定此三角形的形状吗?说明理由;
(4)平面直角坐标中,在x轴上找一点P,使PD+PF的长度最短,求出点P的坐标以及PD+PF的最短长度.
相关试题

