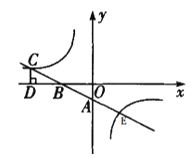
【题目】如图,一次函数y=![]() x-1的图象与坐标轴分别交于A、B两点,与反比例函数y=
x-1的图象与坐标轴分别交于A、B两点,与反比例函数y=![]() 的图象在第二象限的交点为点C,CD⊥x轴,垂足为点D,若C点横坐标为-4,
的图象在第二象限的交点为点C,CD⊥x轴,垂足为点D,若C点横坐标为-4,
(1)反比例函数的关系式及E点坐标;
(2)利用图像,当x<0时,写出![]()
![]() 的解集.
的解集.
参考答案:
【答案】(1)![]() ,E(2,
,E(2,![]() );(2)
);(2)![]() <
<![]()
【解析】
(1)由一次函数与坐标轴的交点求出OA,OB的长,证明△CBD≌△ABO,求出CD=OA,得到C点坐标,从而确定反比例函数关系式,再联立方程组,从而可求出E点坐标;
(2)根据函数图象可以确定不等式![]()
![]() 的解集.
的解集.
(1)在一次函数y=![]() x-1中,令x=0,则y=-1;令y=0,则x=-2.
x-1中,令x=0,则y=-1;令y=0,则x=-2.
∴OA=1,OB=2,
∵C点横坐标为-4,
∴OD=4,
∴DB=DO-BO=4-2=2,
∴OB=DB,
∵CD⊥x轴,
∴∠CDB=∠AOB
又∠CBD=∠ABO
∴△CDB≌△ABO
∴CD=OB=1
∴C(-4,1),
把C(-4,1)代入![]() 得,k=-4,
得,k=-4,
∴![]()
联立方程组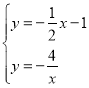 ,解得
,解得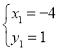 ,
,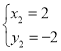
∴E(2,-2);
(2)根据图象可以得出,当![]() <
<![]() 时,
时,![]()
![]() .
.
所以,不等式![]()
![]() 的解集为x<-4.
的解集为x<-4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆内一点到圆周上的点的最大距离是7,最小距离是5,则该圆的半径是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)从A地到B地,某甲走直径AB上方的半圆途径;乙先走直径AC上方半圆的途径,再走直径CB下方半圆的途径,如图1,已知AB=40米,AC=30米,计算个人所走的路程,并比较两人所走路程的远近;
(2)如果甲.乙走的路程图改成图2,两人走的路程远近相同吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为2的正方形ABCD中,AE平分∠DAC,AE交CD于点F,CE⊥AE,垂足为点E,EG⊥CD,垂足为点G,点H在边BC上,BH=DF,连接AH、FH,FH与AC交于点M,以下结论:
①FH=2BH;②AC⊥FH;③S△ACF=1;④CE=
 AF;⑤
AF;⑤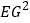 =FGDG,其中正确结论的个数为( )
=FGDG,其中正确结论的个数为( )
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P从
 出发,沿所示方向运动,每当碰到长方形OABC的边时会进行反弹,反弹时反射角等于入射角,当点P第2018次碰到长方形的边时,点P的坐标为______.
出发,沿所示方向运动,每当碰到长方形OABC的边时会进行反弹,反弹时反射角等于入射角,当点P第2018次碰到长方形的边时,点P的坐标为______.
【答案】

【解析】
根据反射角与入射角的定义作出图形;由图可知,每6次反弹为一个循环组依次循环,用2018除以6,根据商和余数的情况确定所对应的点的坐标即可.
解:如图所示:经过6次反弹后动点回到出发点
 ,
,
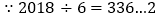 ,
, 当点P第2018次碰到矩形的边时为第337个循环组的第2次反弹,
当点P第2018次碰到矩形的边时为第337个循环组的第2次反弹, 点P的坐标为
点P的坐标为 .
.故答案为:
 .
.【点睛】
此题主要考查了点的坐标的规律,作出图形,观察出每6次反弹为一个循环组依次循环是解题的关键.
【题型】填空题
【结束】
15【题目】为了保护环境,某公交公司决定购买A、B两种型号的全新混合动力公交车共10辆,其中A种型号每辆价格为a万元,每年节省油量为
 万升;B种型号每辆价格为b万元,每年节省油量为
万升;B种型号每辆价格为b万元,每年节省油量为 万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元.
万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元. 请求出a和b;
请求出a和b; 若购买这批混合动力公交车每年能节省
若购买这批混合动力公交车每年能节省 万升汽油,求购买这批混合动力公交车需要多少万元?
万升汽油,求购买这批混合动力公交车需要多少万元? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,∠A=25°,∠B=40°.
(1)求作:⊙O,使⊙O经过A、C两点,且圆心落在AB边上;
(要求:尺规作图,保留作图痕迹,不写作法.)
(2)求证:BC是(1)中所作⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用小立方块搭一个几何体,使它从正面、上面看到的形状图如图所示,从上面看到的形状图的小正方形中的字母表示在该位置小立方块的个数.试回答下列问题:
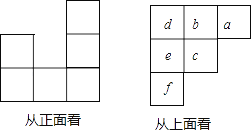
(1)a,b,c各表示几?
(2)这个几何体最少有几个小立方块搭成?最多呢?
(3)当d=e=1,f=2时,画出这个几何体从左面看到的形状图.
相关试题

