Question

【题目】已知，抛物线（a≠0）经过点A（4，4）．

（1）求抛物线的解析式；

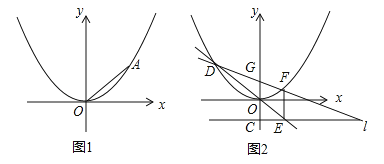
（2）如图1，抛物线上存在点B，使得△AOB是以AO为直角边的直角三角形，请直接写出所有符合条件的点B的坐标： ．

（3）如图2，直线l经过点C（0，﹣1），且平行与x轴，若点D为抛物线上任意一点（原点O除外），直线DO交l于点E，过点E作EF⊥l，交抛物线于点F，求证：直线DF一定经过点G（0，1）．

Answer 1

【答案】（1）；（2）B（﹣4，4）或（﹣8，16）；（3）证明见解析．

【解析】

试题分析：（1）利用待定系数法求出抛物线解析式，（2）分两种情况，先确定出直线OB或AB，和抛物线解析式联立确定出点B的解析式；

（3）先设出点D坐标，确定出点F坐标，进而得出直线DF解析式，将点G坐标代入直线DF看是否满足解析式．

试题解析：（1）∵抛物线（a≠0）经过点A（4，4），∴16a=4，∴a=，∴抛物线的解析式为，（2）存在点B，使得△AOB是以AO为直角边的直角三角形，理由：如图1，∵使得△AOB是以AO为直角边的直角三角形，∴直角顶点是点O，或点A，①当直角顶点是点O时，过点O作OB⊥OA，交抛物线于点B，∵点A（4，4），∴直线OA解析式为y=x，∴直线OB解析式为y=﹣x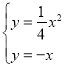，∵，∴（舍）或，∴B（﹣4，4），②当直角顶点为点A，过点A作AB⊥OA，由①有，直线OA的解析式为y=x，∵A（4，4），∴直线AB解析式为y=﹣x+8，∵，解得：（舍）或，∴B（﹣8，16），∴满足条件的点B（﹣4，4）或（﹣8，16）；故答案为：B（﹣4，4）或（﹣8，16）；

（3）证明：设点D（m，），∴直线DO解析式为，∵l∥x轴，C（0，﹣1），令y=﹣1，则x=，∴直线DO与l交于E（，﹣1），∵EF⊥l，l∥x轴，∴F横坐标为，∵点F在抛物线上，∴F（，）．设直线DF解析式为y=kx+b，∴，∴，∴直线DF解析式为，∴点G（0，1）满足直线DF解析式，∴直线DF一定经过点G．