【题目】已知在矩形ABCD中,∠ADC的平分线DE与BC边所在的直线交于点E,点P是线段DE上一定点(其中EP<PD)
(1)如图1,若点F在CD边上(不与D重合),将∠DPF绕点P逆时针旋转90°后,角的两边PD、PF分别交射线DA于点H、G.
①求证:PG=PF;
②探究:DF、DG、DP之间有怎样的数量关系,并证明你的结论.
(2)拓展:如图2,若点F在CD的延长线上(不与D重合),过点P作PG⊥PF,交射线DA于点G,你认为(1)中DE、DG、DP之间的数量关系是否仍然成立?若成立,给出证明;若不成立,请写出它们所满足的数量关系式,并说明理由.

参考答案:
【答案】(1)①证明见解析;②DG+DF=![]() DP;(2)不成立,数量关系式应为:DG﹣DF=
DP;(2)不成立,数量关系式应为:DG﹣DF=![]() DP.
DP.
【解析】(1)①若证PG=PF,可证△HPG≌△DPF,已知∠DPH=∠HPG,由旋转可知∠GPF=∠HPD=90°及DE平分∠ADC得△HPD为等腰直角三角形,即∠DHP=∠PDF=45°、PD=PH,即可得证;
②由△HPD为等腰直角三角形,△HPG≌△DPF知HD=![]() DP,HG=DF,根据DG+DF=DG+GH=DH即可得;
DP,HG=DF,根据DG+DF=DG+GH=DH即可得;
(2)过点P作PH⊥PD交射线DA于点H,先证△HPD为等腰直角三角形可得PH=PD,HD=![]() DP,再证△HPG≌△DPF可得HG=DF,根据DH=DG﹣HG=DG﹣DF可得DG﹣DF=
DP,再证△HPG≌△DPF可得HG=DF,根据DH=DG﹣HG=DG﹣DF可得DG﹣DF=![]() DP.
DP.
解:(1)①∵∠GPF=∠HPD=90°,∠ADC=90°,
∴∠GPH=∠FPD,
∵DE平分∠ADC,
∴∠PDF=∠ADP=45°,
∴△HPD为等腰直角三角形,
∴∠DHP=∠PDF=45°,
在△HPG和△DPF中,
∵∠PHG=∠PDF,PH=PD,∠GPH=∠FPD,
∴△HPG≌△DPF(ASA),
∴PG=PF;
②结论:DG+DF=![]() DP,
DP,
由①知,△HPD为等腰直角三角形,△HPG≌△DPF,
∴HD=![]() DP,HG=DF,
DP,HG=DF,
∴HD=HG+DG=DF+DG,
∴DG+DF=![]() DP;
DP;
(2)不成立,数量关系式应为:DG﹣DF=![]() DP,
DP,
如图,过点P作PH⊥PD交射线DA于点H,
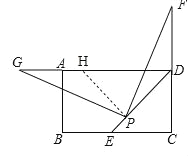

∵PF⊥PG,
∴∠GPF=∠HPD=90°,
∴∠GPH=∠FPD,
∵DE平分∠ADC,且在矩形ABCD中,∠ADC=90°,
∴∠HDP=∠EDC=45°,得到△HPD为等腰直角三角形,
∴∠DHP=∠EDC=45°,且PH=PD,HD=![]() DP,
DP,
∴∠GHP=∠FDP=180°﹣45°=135°,
在△HPG和△DPF中,
∵∠GPH=∠FPD,∠GHP=∠FDP,PH=PD,
∴△HPG≌△DPF,
∴HG=DF,
∴DH=DG﹣HG=DG﹣DF,
∴DG﹣DF=![]() DP.
DP.
“点睛”本题主要考查等腰直角三角形的性质、全等三角形的判定与性质、矩形的性质的综合运用,灵活运用全等三角形的判定与性质将待求证线段关系转移至其他两线段间关系是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种感冒病毒的直径为0.0000000031米,用科学记数法表示为( )
A.3.1×10﹣9米
B.3.1×109米
C.﹣3.1×109米
D.0.31×10﹣8米 -
科目: 来源: 题型:
查看答案和解析>>【题目】夏新同学上午卖废品收入13元,记为+13元,下午买旧书支出9元,记为( )元.
A. +4 B. ﹣9 C. ﹣4 D. +9
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为3cm,圆心O到直线l的距离是4cm,则直线l与⊙O的位置关系是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. ﹣a一定是负数
B. 一个数的绝对值一定是正数
C. 一个数的平方等于16,则这个数是4
D. 平方等于本身的数是0和1
-
科目: 来源: 题型:
查看答案和解析>>【题目】内角为108°的正多边形是( )
A.3
B.4
C.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,抛物线
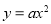 (a≠0)经过点A(4,4).
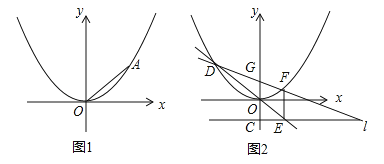
(a≠0)经过点A(4,4).(1)求抛物线的解析式;
(2)如图1,抛物线上存在点B,使得△AOB是以AO为直角边的直角三角形,请直接写出所有符合条件的点B的坐标: .
(3)如图2,直线l经过点C(0,﹣1),且平行与x轴,若点D为抛物线上任意一点(原点O除外),直线DO交l于点E,过点E作EF⊥l,交抛物线于点F,求证:直线DF一定经过点G(0,1).
相关试题

