【题目】某学校为了丰富学生课余生活,决定开设以下体育课外活动项目:A.版画 B.保龄球C.航模 D.园艺种植,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题: 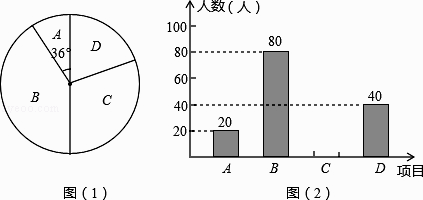
(1)这次被调查的学生共有人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的保龄球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加保龄球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
参考答案:
【答案】
(1)200
(2)解:C项目对应人数为:200﹣20﹣80﹣40=60(人);
补充如图.

(3)解:画树状图得:

∵共有12种等可能的情况,恰好选中甲、乙两位同学的有2种,
∴P(选中甲、乙)= ![]() =
= ![]()
【解析】解:(1)∵A类有20人,所占扇形的圆心角为36°, ∴这次被调查的学生共有:20÷ ![]() =200(人);
=200(人);
故答案为:200;
(1)由A类有20人,所占扇形的圆心角为36°,即可求得这次被调查的学生数;(2)首先求得C项目对应人数,即可补全统计图;(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好选中甲、乙两位同学的情况,再利用概率公式即可求得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=10,AC=2
 ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______.【答案】10或6
【解析】试题解析:根据题意画出图形,如图所示,

如图1所示,AB=10,AC=2
 ,AD=6,
,AD=6,在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=
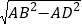 =8,CD=
=8,CD= =2,
=2,此时BC=BD+CD=8+2=10;
如图2所示,AB=10,AC=2
 ,AD=6,
,AD=6,在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=
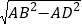 =8,CD=
=8,CD= =2,
=2,此时BC=BD-CD=8-2=6,
则BC的长为6或10.
【题型】填空题
【结束】
12【题目】在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 ______ y2.(填“>”“<”或“=”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①若
 =﹣1,则a、b互为相反数;②若a+b<0,且
=﹣1,则a、b互为相反数;②若a+b<0,且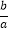 >0,则|a+2b|=﹣a﹣2b;③一个数的立方是它本身,则这个数为0或1;④若﹣1<a<0,则a2>﹣
>0,则|a+2b|=﹣a﹣2b;③一个数的立方是它本身,则这个数为0或1;④若﹣1<a<0,则a2>﹣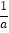 ;⑤若a+b+c<0,ab>0,c>0,则|﹣a|=﹣a,其中正确的个数是( )
;⑤若a+b+c<0,ab>0,c>0,则|﹣a|=﹣a,其中正确的个数是( )A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在等边△ABC中,点E、D分别是AC,BC边的中点,点P为AB边上的一个动点,连接PE,PD,PC,DE.设AP=x,图1中某条线段的长为y,若表示y与x的函数关系的图像大致如图2所示,则这条线段可能是图1中的( )
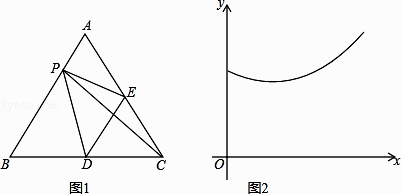
A.线段PD
B.线段PC
C.线段PE
D.线段DE -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂现在的年产值是15万元,计划今后每年增产2万元.
(1)写出年产值y(万元)与年数x之间的函数表达式,并画出图象;
(2)求6年后的年产值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习三角形中位线的性质时,小亮对课本给出的解决办法进行了认真思考:
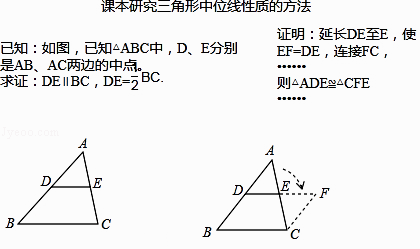 请你利用小亮的发现解决下列问题:
请你利用小亮的发现解决下列问题:
(1)如图1,AD是△ABC的中线,BE交AC于E,交AD于E,且AE=EF,求证:AC=BF. 请你帮助小亮写出辅助线作法并完成论证过程: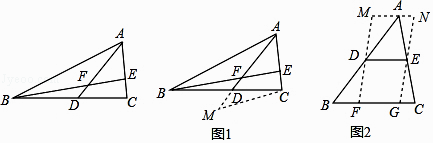
(2)解决问题:如图2,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线,过点D、E作DF∥EG,分别交BC于F、G,过点A作MN∥BC,分别与FE、GE的延长线交于M、N,则四边形MFGN周长的最小值是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】五一期间,小明一家一起去旅游,如图是小明设计的某旅游景点的图纸(网格是由相同的小正方形组成的,且小正方形的边长代表实际长度100m),在该图纸上可看到两个标志性景点A,B.若建立适当的平面直角坐标系,则点A(-3,1),B(-3,-3),第三个景点C(3,2)的位置已破损.
(1)请在图中标出景点C的位置;
(2)小明想从景点B开始游玩,途经景点A,最后到达景点C,求小明一家最短的行走路程(参考数据:
 ≈6,结果保留整数).
≈6,结果保留整数).
相关试题

