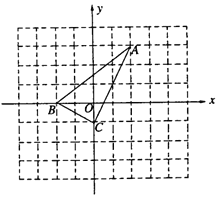
【题目】如图,直角坐标系中的网格由单位正方形构成.△ABC中,A点坐标为(2,3)、B(-2,0)、C(0,-1).
(1)AB的长为_____,∠ACB的度数为______;
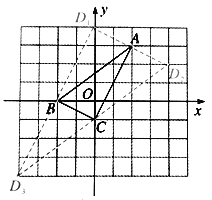
(2)若以A、B、C及点D为顶点的四边形为平行四边形,请写出D点的坐标___________,并在图中画出平行四边形.
参考答案:
【答案】 (1)5 90° (2)(0,4)或(4,2)或(-4,-4),平行四边形如图.
【解析】(1)由勾股定理即可求得AB,BC,AC的值,然后由勾股定理逆定理,可判定△ABC是直角三角形;
(2)首先根据题意画出图形,然后根据图可求得平行四边形中D点的坐标.
(1)根据点A和点B的坐标可知:
AB=![]() =5;
=5;
同理可得BC=![]() =
=![]() ,AC=
,AC=![]() =
=![]() ,
,
所以有(![]() )2+(2
)2+(2![]() )2=52,即
)2=52,即![]()
故△ABC是直角三角形,且∠ACB=90°.
(2)点D的坐标为(0,4)或(4,2)或(-4,-4),所作平行四边形如图所示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为m厘米,宽为n厘米)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )

A. 4m厘米 B. 4n厘米 C. 2(m+n)厘米 D. 4(m-n)厘米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,O为坐标原点,二次函数y=x2+mx+2的图象与x轴的正半轴交于点A,与y轴的正半轴交交于点B,且OA:OB=1:2.设此二次函数图象的顶点为D.

(1)求这个二次函数的解析式;
(2)将△OAB绕点A顺时针旋转90°后,点B落到点C的位置.将上述二次函数图象沿y轴向上或向下平移后经过点C.请直接写出点C的坐标和平移后所得图象的函数解析式;
(3)设(2)中平移后所得二次函数图象与y轴的交点为B1 , 顶点为D1 . 点P在平移后的二次函数图象上,且满足△PBB1的面积是△PDD1面积的2倍,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸中的△ABC经过变换得到△DEF,正确的变换是( )

A.把△ABC向右平移6格
B.把△ABC向右平移4格,再向上平移1格
C.把△ABC绕着点A顺时针旋转90°,再向右平移6格
D.把△ABC绕着点A逆时针旋转90°,再向右平移6格 -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年我县某校有若干名学生参加了七年级数学期末测试,学校随机抽取了考生总数的10%的学生数学成绩,现将他们的成绩分成:A(96分~120分)、B(84分~95分)、C(72分~83分)、D(72分以下)四个等级进行分析,并根据成绩得到如下两个统计图:


(1)在所抽取的考生中,若D级只有3人:
①请估算该校所有考生中,约有多少人数学成绩是D级?
②考生数学成绩的中位数落在__________等级中;
(2)有一位同学在计算所抽取的考生数学成绩的平均数时,其方法是:
 =
= =76.25,
=76.25,问这位同学的计算正确吗?若不正确,请你帮他计算正确的平均数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )

A.a>0
B.当x≥1时,y随x的增大而增大
C.c<0
D.当﹣1<x<3时,y>0
相关试题

