搜索
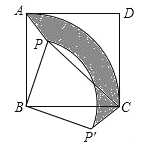
【题目】已知：如图，点P是正方形ABCD内一点，连接PA、PB、PC．
（1）将△PAB绕点B顺时针旋转90°得到△P'CB，若AB=m，PB=n（n＜m）．求△PAB旋转过程中边PA扫过区域（阴影部分）的面积；
（2）若PA=
，PB=
，∠APB=135°，求PC的长．
参考答案：
【答案】（1）
（m2﹣n2）；（2）
．
【解析】试题分析：（1）利用旋转性质，S△ABP=S△CBP′，求扇形面积.(2) 连接PP′,利用旋转，勾股定理求PC值.
试题解析：
解：（1）由旋转的性质可知，S△ABP=S△CBP′，
∴△PAB旋转过程中边PA扫过区域面积=
﹣
=
（m2﹣n2）；
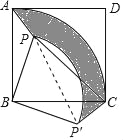
（2）连接PP′，
由旋转的性质可知，∠BP′C=∠APB=135°，∠PBP′=90°，BP′=BP=2
，P′C=PA=
，
∴PP′=
=4，∠PP′C=90°，
∴PC=
=3
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校开展“我最喜爱的一项体育活动”调查，要求每名学生必选且只能选一项，现随机抽查了m名学生，并将其结果绘制成如下不完整的条形图和扇形图．
请结合以上信息解答下列问题：
（1）m= ；
（2）请补全上面的条形统计图；
（3）在图2中，“乒乓球”所对应扇形的圆心角的度数为 ；
（4）已知该校共有1200名学生，请你估计该校约有 名学生最喜爱足球活动．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为保护环境，我市公交公司计划购买A型和B型两种环保节能公交车共10辆．若购买A型公交车1辆，B型公交车2辆，共需400万元；若购买A型公交车2辆，B型公交车1辆，共需350万元．
（1）求购买A型和B型公交车每辆各需多少万元？
（2）预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次．若该公司购买A型和B型公交车的总费用不超过1200万元，且确保这10辆公交车在该线路的年均载客总和不少于680万人次，则该公司有哪几种购车方案？
（3）在（2）的条件下，哪种购车方案总费用最少？最少总费用是多少万元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店经销一种泰山旅游纪念品，4月份的营业额为2000元，为扩大销售量，5月份该商店对这种纪念品打9折销售，结果销售量增加20件，营业额增加700元．
（1）求该种纪念品4月份的销售价格；
（2）若4月份销售这种纪念品获利800元，5月份销售这种纪念品获利多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD是平行四边形，点A（1，0），B（4，1），C（4，3），反比例函数y=
的图象经过点D，点P是一次函数y=mx+3﹣4m（m≠0）的图象与该反比例函数图象的一个公共点；（1）求反比例函数的解析式；
（2）通过计算说明一次函数y=mx+3﹣4m的图象一定过点C；
（3）对于一次函数y=mx+3﹣4m（m≠0），当y随x的增大而增大时，确定点P的横坐标的取值范围，（不必写过程）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在数轴上，已知点
，
分别表示数1，
，那么数轴上表示数
的点应落在( )
A.点
的左边B.线段
上C.点的右边D.数轴的任意位置 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，在△ABC中，AC＝BC，∠ACB＝90°，过点C作CD⊥AB于点D，点E是AB边上一动点(不含端点A，B)，连接CE，过点B作CE的垂线交直线CE于点F，交直线CD于点G．
(1)求证：AE＝CG；
(2)若点E运动到线段BD上时(如图②)，试猜想AE，CG的数量关系是否发生变化，请证明你的结论；
(3)过点A作AH⊥CE，垂足为点H，并交CD的延长线于点M(如图③)，找出图中与BE相等的线段，直接写出答案BE=
相关试题
