【题目】如图甲,在△ABC中,AB=AC,∠BAC=90°.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF. 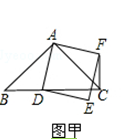
解答下列问题:
(1)当点D在线段BC上时(与点B不重合),如图甲,线段CF、BD之间的位置关系为 , 数量关系为 .
(2)当点D在线段BC的延长线上时,如图乙,①中的结论是否仍然成立,为什么? 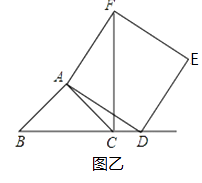
参考答案:
【答案】
(1)垂直;相等
(2)解:当点D在BC的延长线上时①中的结论仍成立.
理由:∵四边形ADEF是正方形,
∴∠DAF=90°,AD=AF,
∴∠BAC=∠DAF=90°,
∴∠BAD+∠DAC=∠CAF+∠DAC,
即∠BAD=∠CAF,
在△BAD和△CAF中,
 ,
,
∴△BAD≌△CAF(SAS),
∴CF=BD,
∴∠B=∠ACF,
∵∠B+∠BCA=90°,
∴∠BCA+∠ACF=90°,
即CF⊥BD
【解析】解:(1)结论:垂直,相等. 理由∵四边形ADEF是正方形,
∴∠DAF=90°,AD=AF,
∵AB=AC,∠BAC=90°,
∴∠BAD+∠DAC=∠CAF+∠DAC=90°,
∴∠BAD=∠CAF,
在△BAD和△CAF中, ,
,
∴△BAD≌△CAF(SAS),
∴CF=BD,
∴∠B=∠ACF,
∴∠B+∠BCA=90°,
∴∠BCA+∠ACF=90°,
即CF⊥BD;
所以答案是:垂直,相等;
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°,以及对正方形的性质的理解,了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足
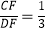 ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=3,AF=4.
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=3,AF=4. 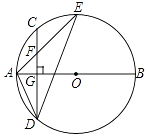
(1)求证:△ADF∽△AED;
(2)求FG的长;
(3)求tan∠E的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了倡导“节约用水,从我做起”,南沙区政府决定对区直属机关300户家庭的用水情况作一次调查,区政府调查小组随机抽查了其中50户家庭一年的月平均用水量(单位:吨),调查中发现每户用水量均在10﹣14吨/月范围,并将调查结果制成了如图所示的条形统计图.

(1)请将条形统计图补充完整;
(2)这50户家庭月用水量的平均数是 ,众数是 ,中位数是 ;
(3)根据样本数据,估计南沙区直属机关300户家庭中月平均用水量不超过12吨的约有多少户?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=6m.

(1)求∠CAE的度数;
(2)求这棵大树折断前的高度?
(结果精确到个位,参考数据: =1.4,
=1.4,  =1.7,
=1.7,  =2.4).
=2.4). -
科目: 来源: 题型:
查看答案和解析>>【题目】某电子厂生产一种新型电子产品,每件制造成本为20元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月获得的利润为400万元?
(3)根据相关部门规定,这种电子产品的销售单价不能高于40元,如果厂商每月的制造成本不超过520万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,以点A(1,0)为圆心,以2为半径的圆与x轴交于B,C两点,与y轴交于D,E两点.
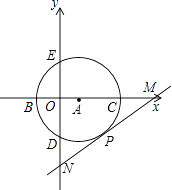
(1)直接写出B,C,D点的坐标;
(2)若B、C、D三点在抛物线y=ax2+bx+c上,求出这个抛物线的解析式及它的顶点坐标.
(3)若圆A的切线交x轴正半轴于点M,交y轴负半轴于点N,切点为P,∠OMN=30°,试判断直线MN是否经过B、C、D三点所在抛物线的顶点?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】α为锐角,且关于x的一元二次方程
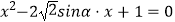 有两个相等的实数根,则α=( )
有两个相等的实数根,则α=( )
A.30°
B.45°
C.30°或150°
D.60°
相关试题

