【题目】α为锐角,且关于x的一元二次方程 ![]() 有两个相等的实数根,则α=( )
有两个相等的实数根,则α=( )
A.30°
B.45°
C.30°或150°
D.60°
参考答案:
【答案】B
【解析】解:方程化为一般形式为:x2﹣2 ![]() sinαx+1=0, ∵关于x的一元二次方程x2﹣2
sinαx+1=0, ∵关于x的一元二次方程x2﹣2 ![]() sinαx+1=0有两个相等的实数根,
sinαx+1=0有两个相等的实数根,
∴△=(2 ![]() sinα)2﹣4=0,即sin2α=
sinα)2﹣4=0,即sin2α= ![]() ,
,
解得,sinα= ![]() ,sinα=﹣
,sinα=﹣ ![]() (舍去).
(舍去).
∴α=45°.
故选B.
【考点精析】掌握求根公式和特殊角的三角函数值是解答本题的根本,需要知道根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”.
-
科目: 来源: 题型:
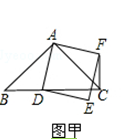
查看答案和解析>>【题目】如图甲,在△ABC中,AB=AC,∠BAC=90°.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
解答下列问题:
(1)当点D在线段BC上时(与点B不重合),如图甲,线段CF、BD之间的位置关系为 , 数量关系为 .
(2)当点D在线段BC的延长线上时,如图乙,①中的结论是否仍然成立,为什么?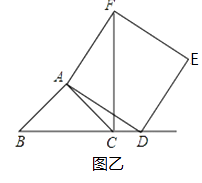
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电子厂生产一种新型电子产品,每件制造成本为20元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月获得的利润为400万元?
(3)根据相关部门规定,这种电子产品的销售单价不能高于40元,如果厂商每月的制造成本不超过520万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,以点A(1,0)为圆心,以2为半径的圆与x轴交于B,C两点,与y轴交于D,E两点.
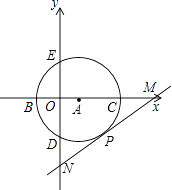
(1)直接写出B,C,D点的坐标;
(2)若B、C、D三点在抛物线y=ax2+bx+c上,求出这个抛物线的解析式及它的顶点坐标.
(3)若圆A的切线交x轴正半轴于点M,交y轴负半轴于点N,切点为P,∠OMN=30°,试判断直线MN是否经过B、C、D三点所在抛物线的顶点?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某班计划购买篮球和排球若干个,买4个篮球和3个排球需要410元;买2个篮球和5个排球需要310元.
(1)篮球和排球单价各是多少元?
(2)若两种球共买30个,费用不超过1700元,篮球最多可以买多少个?
(3)如果购买这两种球刚好用去520元,问有哪几种购买方案?
-
科目: 来源: 题型:
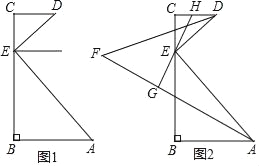
查看答案和解析>>【题目】如图1,线段AB⊥BC于点B,CD⊥BC于点C,点E在线段BC上,且AE⊥DE.
(1)求证:∠EAB=∠CED;
(2)如图2,AF、DF分别平分∠BAE和∠CDE,EH平分∠DEC交CD于点H,EH的反向延长线交AF于点G.
①求证EG⊥AF;
②求∠F的度数.(提示:三角形内角和等于180度)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分9分)小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发
的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路
以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1 m,小明爸爸与家之间的距
离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.
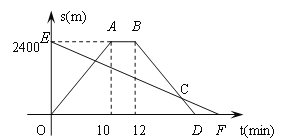
(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
相关试题

